Расчёт сопел современных ракетных двигателей / Хабр

Принято считать, что сопло Лаваля – это техническое устройство, предназначенное исключительно для разгона газовых потоков до сверхзвуковых скоростей.

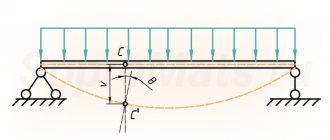
Возьмем рисунок из статьи Википедии. (Рис.1.), на котором схематично показано сечение сопла, а также динамика давления, температуры и скорости газового потока вдоль оси сопла.

Рис.1 Иллюстрация работы сопла Лаваля. По мере движения газа по соплу, его абсолютная температура Т и давление Р снижаются, а скорость V возрастает. М — число Маха.

Суживающая часть сопла называется конфузором, а расширяющая – диффузором. Хочу обратить внимание на соотношение длин конфузора и диффузора. Диффузор по длине больше конфузора. И хотя на этот факт в разных источниках никто не обращает внимание, думаю, что это важный параметр, значение которого необходимо соблюдать. Причем, если проектировать сопло Лаваля для газового и парового потока, то, действительно, длина конфузора должна быть меньше длины диффузора.

Не знаю, как объясняют этот факт ученые люди, но как русский дилетант могу предположить, что это связано с некими газовыми законами. Если сравнивать сопло Лаваля и самый обыкновенный ДВС (двигатель внутреннего сгорания), то можно заметить, что между ними есть некая аналогия – чередование фаз сжатия и разряжения, что в итоге позволяет выделиться внутренней энергии газа (топлива). В ДВС имеется 4 фазы – две изотермические и две адиабатические. В сопле Лаваля, похоже, есть только две фазы – адиабатическое сжатие и изотермическое расширение.

Сжатие осуществляется в конфузоре. И для адиабатического процесса он должен быть коротким. Изотермическое расширение происходит в диффузоре, поэтому для приближения процесса к изотермическому диффузор должен быть длинным, гораздо длиннее конфузора.

Говорить об идентичности сжатия и разряжения газа вдоль центральной оси сопла Лаваля, конечно, надо с некой долей условности, так как быстротечность процессов в нём не позволяет осуществляться процессу теплообмена между струёй газа и окружающей средой. Но кто говорит об окружающей среде? Ведь надо же в первую очередь объяснить, откуда топливо при своём сгорании черпает ту энергию, которая позволяет забрасывать спутники и космические корабли на орбиту Земли и даже дальше? Умные люди утверждают, что это так называемая внутренняя энергия топлива, но сам механизм этого процесса мудро замалчивают, ссылаясь на некие законы природы, открытые экспериментальным путём.

Мне, как дилетанту, остается предположить, что внутренняя энергия топлива – это ответная реакция эфирной и газовой среды на движущийся вдоль сопла Лаваля поток газа. Вначале эту совместную среду подвергают адиабатическому сжатию, потом – изотермическому расширению. И в ответ эфиро-атомная смесь отвечает выбросом инфракрасного излучения и разного рода ударными волнами. И этот ответ в большой степени зависит от состава газа. Разные газы дают разные ответные реакции. Но при любом газе важно учитывать участие в этом процессе эфирной среды.

Сопло Лаваля можно даже рассматривать в качестве простого варианта теплового насоса.

Соединив два сопла Лаваля, Шестеренко получил свой насадок. Здесь можно познакомиться с одним его патентом. А здесь с другим патентом. При желании любой пользователь может найти еще патенты Шестеренко на насадки и супернасадки разной конструкции. Думаю, что в последние годы никто в открытую не заявляет, что он использует насадки Шестеренко в тех или иных производственных процессах. Но, похоже, эти конструкции уже активно работают по всему миру, в том числе и в России.

Сопло Лаваля некоторые изобретатели пытались использовать в теплогенераторах в качестве кавитатора. Как известно, вода при высоких скоростях начинает парить прямо в потоке, образуя множество мелких пузырьков пара, которые схлопываясь, порождают массу интересных феноменов, одним из которых является нагрев воды. Правда, при использовании классических сопел Лаваля, которые хорошо работают в газовых потоках, в водном потоке кавитация приводила к слабому сверхъединичному эффекту – 120-200%. Это, конечно, требовало пересмотра некоторых положений физики, но с другой стороны, такой КУМ (коэффициент усиления мощности) не позволял надеяться на создании мощных энергогенераторов и всегда таил в себе угрозу, что найдется желающий охаять такой скромный результат, списав всё это на невежество первооткрывателей и несовершенство измерительной методики или техники. Именно по такому сценарию подвергались критике первые опыты по холодному ядерному синтезу. Такая же реакция была на создателей первых теплогенераторов, например, Потапова. Поэтому для водных потоков требовалась совсем другая форма сопел Лаваля. И такие попытки были проведены.

Остальную информацию желающие могут получить непосредственно из самого патента. Нам же важно понять, что для легко вскипающих жидкостей сопло Лаваля должно иметь конструкцию отличную от тех, что хорошо работают с газовыми потоками. И, скорее всего, для каждого конкретного газа или жидкости, а также для выбранных режимов работы, следует создавать «своё» сопло Лаваля.

Сопло Лаваля для легкокипящей жидкости, например воды, должно учитывать такой факт, как увеличение объема массы в случае формирования в жидкости двух фаз – жидкости и пара. Ибо пар занимает при давлении в 1 атмосферу объем в сотни раз больше. Для воды этот показатель равен примерно 600-700. Поэтому для увеличения объема потока в два раза требуется, чтобы в пар превратилась незначительная часть жидкости, буквально 1-3%. При этом имеет место рост давления, возрастает силовое воздействие смеси. И этот результат достается даром, как проявление неких законов Природы – законов фазового перехода, роль Эфира в которых еще просто не изучена.

Именно по этой причине у меня и появилась уверенность в том, что сопло Лаваля – это сверхъединичное устройство, которое позволяет использовать не только теплотворную способность топлива, как это имеет место в ДВС, Дизеле или двигателе Стирлинга, но также и ответную реакцию среды, проявлением которой является не только дополнительное инфракрасное излучение и ударные волны, но и масса других интересных эффектов.

Принцип работы сопла Лаваля:

Ниже на иллюстрации показана работа сопла Лаваля.

По мере движения газа по соплу, его абсолютная температура Т и давление Р снижаются, а скорость V возрастает. Внутренняя энергия газа преобразуется в кинетическую энергию его направленного движения. КПД этого преобразования в некоторых случаях (например, в соплах современных ракетных двигателей) может превышать 70 %. М – число Маха (скорость звука).

На сужающемся, докритическом участке сопла движение газа происходит с дозвуковыми скоростями (М газа достигает звуковой (М = 1). На расширяющемся, закритическом участке, газовый поток движется со сверхзвуковыми скоростями (М > 1).

Суживающая часть сопла называется конфузором, а расширяющая – диффузором. Диффузор по длине всегда больше конфузора. Иногда длина диффузора превышает длину конфузора в 250 раз. Удлинение диффузора способствует увеличению скорости истечения газа из сопла, а соответственно и тяги.

скорость истечения расчет работа истечение из сопла лаваля сопло лаваля принцип работы чертеж купить температура для воздуха своими руками формулы для воды калькулятор википедия размеры

Источник

Принцип работы сопла Лаваля

По мере движения газа по соплу его абсолютная температура Т и давление Р снижаются, а скорость V возрастает.

Внутренняя энергия газа преобразуется в кинетическую энергию его направленного движения.

КПД этого преобразования в некоторых случаях (например, в соплах современных ракетных двигателей) может превышать 70 %. М – число Маха (скорость звука).

На сужающемся, докритическом участке сопла движение газа происходит с дозвуковыми скоростями (М 1).

Элементарная теория сопла Лаваля

Влияние сжимаемости на форму трубок тока.

Рассмотрим, как влияет сжимаемость на форму трубок тока при установившемся движении газа. Предположим, что трубка тока тонкая, и характеристики движения в разных точках каждого сечения одинаковы. Пусть – площадь произвольного поперечного сечения трубки тока, причем сечение перпендикулярно к скорости движения частиц газа.

Если жидкость однородная и несжимаемая, то из уравнения неразрывности следует, что массовый и объемный расходы через трубку тока постоянны, т.е. ; и

т.е. чем больше скорость, тем меньше сечение.

Для сжимаемой жидкости плотность зависит от скорости. Для обратимых адиабатических течений совершенного газа

Подставляя это выражение в (7.39), можно получить зависимость и найти форму трубок тока. График приведен на рис. 7.15.

Спроектируем уравнение движения Эйлера на линию тока и при установившемся движении

где вдоль линии тока. Для адиабатических движений, как было указано ранее, совпадает со скоростью звука, определяемой как (в общем случае величина отлична от скорости звука, но в последующем для неадиабатических движений играет роль скорости звука). Таким образом, вдоль линии тока имеем

Таким образом, в дозвуковом потоке поперечное сечение трубки тока с ростом скорости уменьшается. Максимальная скорость, которая может быть достигнута при дозвуковом потоке в сужающейся трубке тока, равна скорости звука.

Насадок, состоящий только лишь из сужающегося участка (рис. 7.17), называется простым соплом. Наибольшая скорость, которую можно получить, выпуская адиабатически газ через простое сопло, равна скорости звука, которая достигается в наиболее узком сечении (на срезе сопла).

Рассмотрим, как зависит массовый расход газа через сопло от отношения давлений при постоянных значениях температуры и давления в сосуде, когда отсутствует теплообмен между газом и окружающей средой.

При на основе (7.43) получим, что (точка на рис. 7.19).

Критический расход, согласно (7.30) и (7.42), будет равен

При дальнейшем понижении противодавления течение внутри сопла перестает меняться, и расход также остается неизменным и равным критическому. Неизменность расхода объясняется тем, что слабые возмущения (а значит, и небольшие изменения противодавления) распространяются по частицам среды со скоростью звука. Поэтому при достижении критического режима (когда сами частицы на срезе сопла имеют скорость, равную скорости звука) частицы, находящиеся внутри сопла, “не знают” о том, что происходит вне сопла (возмущения сносятся потоком частиц газа, и поток как бы запирает сопло).

Замечание. Изменение противодавления будет сказываться на течении газа вне сопла: в свободной струе вне сопла скорость при понижении может стать сверхзвуковой, но поток в свободной струе не будет однородным (скорость в потоке существенно меняется по сечению струи).

При истечении сжимаемого газа из тонкого отверстия скорость потока, как было показано выше, не может быть больше скорости звука. Достижение сверхзвуковой скорости истечения, как показали опыты Г. Лаваля (1845 – 1913), получается только при изменении конфигурации отверстия. В его экспериментах скорость истечения превышала скорость звука тогда, когда на выходе из сосуда устанавливалась специальная насадка, которая впоследствии была названа соплом Лаваля.

Сопло Лаваля

Сопло́ Лава́ля

— техническое приспособление, разгоняющее проходящий по нему газовый поток до сверхзвуковых скоростей. Широко используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.

Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами. Эффективные сопла современных ракетных двигателей профилируются на основании газодинамических расчётов.

Сопло было предложено в 1890 г. шведским изобретателем Густафом де Лавалем для паровых турбин.

Приоритет Годдарда на применение сопла Лаваля для ракет подтверждается рисунком в описании изобретения в патенте США U.S. Patent 1 102 653 от 7 июля 1914 г., на двухступенчатую твердотопливную ракету, заявленном в октябре 1913 г.

Скорость истечения газа из сопла

Из уравнения состояния идеального газа, и баланса энергии в газовом потоке выводится формула расчёта линейной скорости истечения газа из сопла Лаваля: [1]
(4)
— Скорость газа на выходе из сопла, м/с, — Абсолютная температура газа на входе, — Универсальная газовая постоянная Дж/(киломоль·К), — молярная масса газа, кг/киломоль, — Показатель адиабаты , — Удельная теплоёмкость при постоянном давлении, Дж/(киломоль·К), — Удельная теплоёмкость при постоянном объеме, Дж/(киломоль·К),

Применение

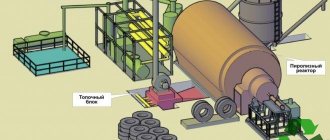
В промышленности и в быту кавитационные теплогенераторы нашли реализацию в самых различных сферах деятельности. В зависимости от поставленных задач они применяются для:

Отопления – внутри установок происходит преобразование механической энергии в тепловую, благодаря чему нагретая жидкость двигается по системе отопления. Следует отметить, что кавитационные теплогенераторы могут отапливать не только промышленные объекты, но и целые поселки.
Нагревание проточной воды – кавитационная установка способна быстро нагревать жидкость, за счет чего может легко заменять газовую или электрическую колонку.
Смешение жидких веществ – за счет разрежения в слоях с получением мелких полостей такие агрегаты позволяют добиться надлежащего качества перемешивания жидкостей, которые естественным образом не совмещаются из-за разной плотности.

Функционирование в среде

При работе сопла Лаваля в непустой среде (чаще всего речь идет об атмосфере) сверхзвуковое течение может возникнуть только при достаточно большом избыточном давлении газа на входе в сопло по сравнению с давлением окружающей среды.

При возникновении сверхзвукового течения давление газа на выходном срезе сопла может оказаться даже меньше давления окружающей среды (вследствие перерасширения

газа при движении по соплу). Такой поток может оставаться стабильным, поскольку давление окружающей среды (пока оно ненамного превышает давление газа на срезе сопла) не может распространяться против сверхзвукового потока. [
источник не указан 980 дней
]

В общем случае удельный импульс сопла Лаваля (при работе как в среде, так и в пустоте) определяется выражением:
(5)
Здесь

— скорость истечения газа из сопла, определяемая по формуле (4); — площадь среза сопла; — давление газа на срезе сопла; — давление окружающей среды; — секундный массовый расход газа через сопло.

Из выражения (5) следует, что удельный импульс и, соответственно, тяга ракетного двигателя в пустоте (при

) всегда выше, чем в атмосфере. Это находит отражение в характеристиках реальных ракетных двигателей: обычно для двигателей, работающих в атмосфере, указываются по два значения для удельного импульса и тяги —
в пустоте
и
на уровне моря
(например, РД-107).

Зависимость характеристик двигателя от давления газа на срезе сопла

носит более сложный характер: как следует из уравнения (4), растёт с убыванием , а добавка — убывает, и при становится отрицательной.

При фиксированном расходе газа и давлении на входе в сопло величина

зависит только от площади среза сопла, которую обычно характеризуют относительной величиной —
степенью расширения
сопла — отношением площади конечного среза к площади критического сечения. Чем больше степень расширения сопла, тем меньше давление , и тем больше скорость истечения газа .

Рассматривая соотношение давления на срезе сопла и давления окружающей среды, выделяют следующие случаи. [2]

Вышесказанное объясняет то обстоятельство, что ракетные двигатели, работающие в плотных слоях атмосферы, как правило, имеют степень расширения меньшую, чем двигатели, работающие в пустоте. Например, у двигателя F-1 первой ступени носителя Сатурн-5 степень расширения составляет 16:1, а RL 10B-2 — двигатель, используемый NASA на ускорителях межпланетных зондов, имеет степень расширения равную 250:1.

Стремление добиться эффективной работы двигателя как на Земле, так и на высоте заставляет конструкторов искать технические решения, позволяющие достигнуть эту цель. Одним из таких решений явился подвижный сопловой насадок

— «продолжение» сопла, которое пристыковывается к нему по достижении ракетой разреженных слоёв атмосферы, увеличивая, таким образом, степень расширения сопла. Схема действия насадка изображена на рисунке справа. Эта схема была практически реализована, в частности, в конструкции двигателя НК-33-1.

Проблема оптимизации степени расширения сопла очень актуальна и при разработке авиационных реактивных двигателей, поскольку самолёт предназначен для полётов в широком диапазоне высот, а от удельного импульса его двигателей в сильной мере зависит экономичность и, следовательно, дальность полёта. В современных турбореактивных двигателях применяются регулируемые сопла

Лаваля. Такие сопла состоят из продольных пластин, имеющих возможность перемещения друг относительно друга, со специальным механизмом с гидравлическим или пневматическим приводом, позволяющим в полёте изменять площадь выходного и/или критического сечений, и, таким образом, добиваться оптимальной степени расширения сопла при полёте на любой высоте. Регулирование площади проходных сечений выполняется, как правило, автоматически специальной системой управления. Этот же механизм позволяет по команде пилота изменять в некоторых пределах и направление реактивной струи, а следовательно, направление
вектора тяги
, что существенно повышает маневренность самолёта.

Плюсы и минусы

В сравнении с другими теплогенераторами, кавитационные агрегаты отличаются рядом преимуществ и недостатков.

К плюсам таких устройств следует отнести:

Куда более эффективный механизм получения тепловой энергии;
Расходует значительно меньше ресурсов, чем топливные генераторы;
Может применяться для обогрева как маломощных, так и крупных потребителей;
Полностью экологичен – не выделяет в окружающую среду вредных веществ во время работы.

К недостаткам кавитационных теплогенераторов следует отнести:

Сравнительно большие габариты – электрические и топливные модели имеют куда меньшие размеры, что немаловажно при установке в уже эксплуатируемом помещении;
Большая шумность за счет работы водяного насоса и самого кавитационного элемента, что затрудняет его установку в бытовых помещениях;
Неэффективное соотношение мощности и производительности для помещений с малой квадратурой (до 60м2 выгоднее использовать установку на газу, жидком топливе или эквивалентной электрической мощности с нагревательным тэном).\