Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Основные понятия механики сплошных сред
ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНЫХ СРЕД Основные объекты теоретической механики • Материальная точка • Дискретные системы материальных точек • Абсолютно твердые тела Основные объекты механики сплошных сред • Газообразные среды • Жидкие среды • Твердые деформируемые тела Характеристики сплошных сред • Однородность (неоднородность) относительно некоторого свойства • Изотропность (анизотропность) относительно некоторого свойства Типы сил в механике сплошных сред • Массовые силы действуют на все элементы сплошной среды.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
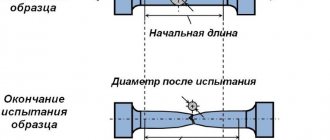
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_{0}\) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
\[ \large L_{0} + \Delta L = L \]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_{0}\).
\[ \large \boxed{ \Delta L = L — L_{0} }\]
\( L_{0} \left(\text{м} \right) \) – начальная длина пружины;
\( L \left(\text{м} \right) \) – конечная длина растянутой пружины;
\( \Delta L \left(\text{м} \right) \) – кусочек длины, на который растянули пружину;
Величину \( \Delta L \) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
\[ \large \boxed{ \frac{\Delta L }{ L_{0}} = \frac{ L — L_{0}}{L_{0} } = \varepsilon } \]
\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Закон гука определение и формула
Министерство образования АР Крым Таврический Национальный Университет им.
Вернадского Исследование физического закона ЗАКОН ГУКА Выполнил: студент 1 курса физического факультета гр.
Ф-111 Потапов Евгений Симферополь-2010 План:
- Каким образом был открыт закон: на основе опытных данных или теоретически.
- Примеры использования закона и учета действия закона на практике.
- Формулировка закона
- Литература.
- Математическое выражение закона.
- Связь между какими явлениями или величинами выражает закон.
- Опытные факты на основе которого был сформулирован закон.
- Опыты, подтверждающие справедливость закона, сформулированного на основе теории.
Связь между какими явлениями или величинами выражает закон: Закон Гука связывает такие явления, как напряжение и деформацию твердого тела, модуль силы упругости и удлинение.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_{\text{упр}} \) силой упругости.
\[ \large \boxed{ F_{\text{упр}} = k \cdot \Delta L }\]
Эту формулу назвали законом упругости Гука.
\( F_{\text{упр}} \left( H \right) \) – сила упругости;
\( \Delta L \left(\text{м} \right) \) – удлинение пружины;
\( \displaystyle k \left(\frac{H}{\text{м}} \right) \) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
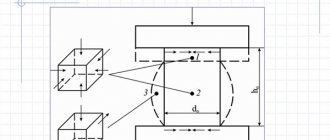
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
\[ \large F_{\text{упр}} — m \cdot g = 0 \]
Подставим в это уравнение выражение для силы упругости
\[ \large k \cdot \Delta L — m \cdot g = 0 \]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:
\[ \large \boxed{ k = \frac{ m \cdot g }{\Delta L} }\]
\(g\) – ускорение свободного падения, оно связано с силой тяжести.
Теоретическая механика и сопромат
Законом Гука называют базовую зависимость в механике, устанавливающую взаимосвязь между и соответствующими им . Закон был открыт в 1660 году английским ученым . Проведя серию экспериментов с пружин, Гук заметил, что изменение их длины прямо пропорционально растягивающей (сжимающей) их силе.
Свои наблюдения он оформил в виде закона: «Какова сила, таково и удлинение».
Современная формулировка закона существенно отличается от оригинала и зависит от дисциплины, в которой рассматривается зависимость от усилий.
Подробнее про закон Гука смотрите в нашем видео:
В современных учебниках физики Закон Гука имеет вид:
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину \(\Delta L\). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом \(mg\).
Одна пружина:
\[ \large k_{1} \cdot \Delta L = m \cdot g \]
Две параллельные пружины:
\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_{\text{параллел}} \cdot \Delta L \cdot \frac{1}{2}= k_{1} \cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
\[ \large k_{\text{параллел}} \cdot \frac{1}{2}= k_{1} \]
Умножим обе части полученного уравнения на число 2:
\[ \large \boxed{ k_{\text{параллел}} = 2k_{1} } \]
Коэффициент жесткости \(k_{\text{параллел}}\) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину \(\Delta L\). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину \(\Delta L\).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом \(mg\).
Одна пружина:
\[ \large k_{1} \cdot \Delta L = m \cdot g \]
Две последовательные пружины:
\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_{\text{послед}} \cdot \Delta L \cdot 2 = k_{1} \cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
\[ \large k_{\text{послед}} \cdot 2 = k_{1} \]
Разделим обе части полученного уравнения на число 2:
\[ \large \boxed{ k_{\text{послед}} = \frac{k_{1}}{2} } \]
Коэффициент жесткости \(k_{\text{послед}}\) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Обобщенный закон Гука
Законом Гука обычно называют линейные соотношения между компонентами деформаций и компонентами напряжений.
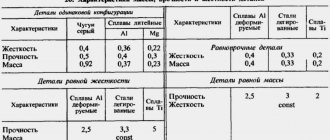
Возьмем элементарный прямоугольный параллелепипед с гранями, параллельными координатным осям, нагруженный нормальным напряжением σх, равномерно распределенным по двум противоположным граням (рис. 1). При этом σy = σz = τхy = τхz = τyz = 0.
Рис. 1 Вплоть до достижения предела пропорциональности относительное удлинение дается формулой где Е — модуль упругости при растяжении.
Для стали Е = 2*105 МПа, поэтому деформации очень малы и измеряются в процентах или в 1*105 (в тензометрических приборах, измеряющих деформации). Удлинение элемента в направлении оси х сопровождается его сужением в поперечном направлении, определяемом компонентами деформаций где μ – константа, называемая коэффициентом поперечного сжатия или коэффициентом Пуассона.
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину \(\Delta L \) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
\[ \large \boxed{ E_{p} = \frac{k}{2} \cdot \left( \Delta L \right)^{2} }\]
\( E_{p} \left( \text{Дж} \right)\) – потенциальная энергия сжатой или растянутой пружины;
\( \Delta L \left(\text{м} \right) \) – удлинение пружины;
\( \displaystyle k \left(\frac{H}{\text{м}} \right) \) – коэффициент жесткости (упругости) пружины.
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
9.8. Формулы обобщенного закона Гука
Гипотеза пластичности Хубера—Мизеса Согласно этой гипотезе переход тела из упругого состояния в пластическое происходит, когда
достигнет некоторого постоянного значения. Возникает вопрос: почему гипотеза Мизеса, приводящая к более сложному выражению для
, принимается наряду с гипотезой Сен—Венана.
Она достигает максимума при чистом сдвиге, когда