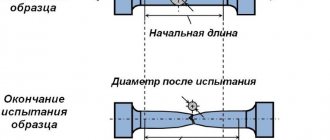
Модуль Юнга (синонимы: модуль упругости I рода, модуль продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 10 9 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.
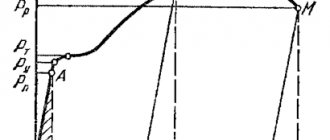
Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σ пц
(тангенсу угла α наклона участка пропорциональности к оси деформаций ε ).
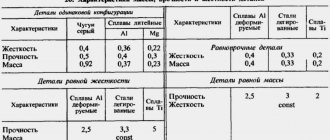
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Читать также: Станок для перемотки пожарных рукавов своими руками
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Модуль Юнга в действии
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п — число пи, равное 3,14, а r — радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g — ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d — относительная деформация в упругой области.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
https://youtube.com/watch?v=YjfWehCZnf8
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия — явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Что представляет собой медь
Cuprum
Одним из наиболее распространенных цветных металлов, используемых в промышленности, является медь, ее название на латинском Cuprum, в честь острова Кипра, где ее добывали греки много тысяч лет назад. Это один из семи металлов, которые были известны еще в глубокой древности, из него делали украшения, посуду, деньги, орудия.
Историками даже назван период (с IV по III тысячелетие до нашей эры) Медным Веком. Д. И. Менделеев поставил этот металл на 29-е место в своей таблице, после водорода, поскольку медь не вытесняет его из кислотной среды. Медь — цветной металл, который имеет уникальные физические, механический, химические свойства.
Плотность меди в кг м³ является одной из важнейших характеристик, с ее помощью определяется вес будущего изделия.
Как определяется плотность
Плотность любого вещества — показатель отношения массы к общему объему. Наиболее распространенной системой измерения величины плотности является килограмм на кубический метр. Для меди этот показатель равен 8,93 кг/м³. Поскольку существуют различные марки металла, которые различаются в зависимости от примесей других веществ, общий показатель плотности может изменяться. В данном случае уместней использовать другую характеристику — удельный вес. В измерительных системах этот показатель выражается в разных величинах:
Формула определения плотности вещества
- система СГС — дин/см³;
- система СИ — н/м³;
- система МКСС — кг/м³
При этом для перевода величин можно использовать следующую формулу:
1 н/м³ = 1 дин/см³ = 0,102 кг/м³.
Удельный вес — важный показатель при производстве различных материалов, содержащих медь, особенно когда речь идет о ее сплавах. Это величина отношения массы меди в общем объеме сплава.
Рассмотреть как применяется этот показатель на практике, можно на примере расчета веса 25 медных листов, размером 2000*1000 мм, толщиной 5 мм. Для начала определим объем листа — 5 мм * 2000 мм * 1000 мм = 10000000 мм3 или 10 000 см³.
Удельный вес меди 8, 94 гр/см³
Рассчитываем вес меди в одном листе — 10 000 * 8,94 = 89 400 гр или 89, 40 кг.
Масса медного проката в общем количестве материала — 89, 40 * 25 = 2 235 кг.
Эта схема расчета применяется и при переработке лома металла.
Основные свойства
Выплавка меди из руды
Медь, как металл, получается при выплавке руды, в природе сложно найти чистые самородки в основном обогащение и добыча осуществляется из:
- халькозиновой руды, в которой содержание меди около 80%, этот вид часто называют медным блеском;
- бронитовой руды, здесь содержание металла до 65%
- ковеллиновой руды — до 64%.
По своим физическим свойствам медь представляет собой красного цвета металл, в разрезе может присутствовать розовый отлив, относится к тяжелым металлам, поскольку имеет высокую плотность.
Отличительной характеристикой является электропроводность. Благодаря этому металл широко применяется при изготовлении кабелей и электропроводов. По этому показателю медь уступает только серебру, кроме того, имеется ряд других физических характеристик:
- твердость — по шкале Бринделя равняется 35 кгс/мм²;
- упругость — 132000 Мн/м²;
- линейное термическое расширение — 0,00000017 единицы;
- относительное удлинение — 60%;
- температура плавления — 1083 ºС;
- температура кипения — 2600 ºС;
- коэффициент теплопроводности — 335 ккал/м*ч*град.
Модуль сдвига
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 — результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η — коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Модуль упругости дерева
Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.
Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
Оксид алюминия Al2O3
Оксид алюминия Al2O3, называемый также глиноземом, встречается в природе в кристаллическом виде, образуя минерал корунд. Корунд обладает очень высокой твердостью. Его прозрачные кристаллы, окрашенные в красный или синий цвет, представляют собой драгоценные камни — рубин и сапфир. В настоящее время рубины получают искусственно, сплавляя с глиноземом в электрической печи. Они используются не столько для украшений, сколько для технических целей, например, для изготовления деталей точных приборов, камней в часах и т.п. Кристаллы рубинов, содержащих малую примесь Cr2O3, применяют а качестве квантовых генераторов — лазеров, создающих направленный пучек монохроматического излучения.
Корунд и его мелкозернистая разновидность, содержащая большое количество примесей — наждак, применяются как абразивные материалы.