Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
- Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
- Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
- Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
- Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
- Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
- Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
- И напоследок коэффициент Пуассона для стали равен значению 0,3
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
| Материал | Показатели модуля упругости (Е, G; Н*м2, кг/см^2, МПа) |
| Сталь | 20,6*10^10 ньютон*метр^2 |
| Сталь углеродистая | Е=(2,0…2,1)*10^5 МПа; G=(8,0…8,1)*10^4 МПа |
| Сталь 45 | Е=2,0*10^5 МПа; G=0,8*10^5 МПа |
| Сталь 3 | Е=2,1*10^5 МПа; G=0,8*10^5 МПа |
| Сталь легированная | Е=(2,1…2,2)*10^5 МПа; G=(8,0…8,1)*10^4 МПа |
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.
Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Соединения меди
Оксид меди (I) Cu2O3 и закись меди (I) Cu2O, как и другие соединения меди (I) менее устойчивы, чем соединения меди (II). Оксид меди (I), или закись меди Cu2O в природе встречается в виде минерала куприта. Кроме того, она может быть получена в виде осадка красного оксида меди (I) в результате нагревания раствора соли меди (II) и щелочи в присутствии сильного восстановителя.
Оксид меди (II), или окись меди, CuO — черное вещество, встречающееся в природе (например в виде минерала тенерита). Его получают прокаливанием гидроксокарбоната меди (II) (CuOH)2CO3 или нитрата меди (II) Cu(NO2)2. Оксид меди (II) хороший осислитель.
Гидроксид меди (II) Cu(OH)2 осаждается из растворов солей меди (II) при действии щелочей в виде голубой студенистой массы. Уже при слабом нагревании даже под водой он разлагается, превращаясь в черный оксид меди (II). Гидроксид меди (II) — очень слабое основание. Поэтому растворы солей меди (II) в большинстве случаев имеют кислую реакцию, а со слабыми кислотами медь образует основные соли.
Сульфат меди (II) CuSO4 в безводном состоянии представляет собой белый порошок, который при поглощении воды синеет. Поэтому он применяется для обнаружения следов влаги в органических жидкостях. Водный раствор сульфата меди имеет характерный сине-голубой цвет. Эта окраска свойственна гидратированным ионам [Cu(H2O)4]2+, поэтому такую же окраску имеют все разбавленные растворы солей меди (II), если только они не содердат каких-либо окрашенных анионов. Из водных растворов сульфат меди кристаллизуется с пятью молекулами воды, образуя прозрачные синие кристаллы медного купороса. Медный купорос применяется для электролитического покрытия металлов медью, для приготовления минеральных красок, а также в качестве исходного вещества при получении других соединений меди. В сельском хозяйстве разбавленный раствор медного купороса применяется для опрыскивания растений и протравливания зерна перед посевом, чтобы уничтожить споры вредных грибков.
Хлорид меди (II) CuCl2. 2H2O. Образует темно-зеленые кристаллы, легко растворимые в воде. Очень концентрированные растворы хлорида меди (II) имеют зеленый цвет, разбавленные — сине-голубой.
Нитрат меди (II) Cu(NO3)2.3H2O. Получается при растворении меди в азотной кислоте. При нагревании синие кристаллы нитрата меди сначала теряют воду, а затем легко разлагаются с выделением кислорода и бурого диоксида азота, переходя в оксид меди (II).
Гидроксокарбонат меди (II) (CuOH)2CO3. Встречается в природе в виде минерала малахита, имеющего красивый изумрудно-зеленый цвет. Искусственно приготовляется действием Na2CO3 на растворы солей меди (II). 2CuSO4 + 2Na2CO3 + H2O = (CuOH)2CO3v + 2Na2SO4 + CO2^ Применяется для получения хлорида меди (II), для приготовления синих и зеленых минеральных красок, а также в пиротехнике.
Ацетат меди (II) Cu (CH3COO)2.H2O. Получается обработкой металлической меди или оксида меди (II) уксусной кислотой. Обычно представляет собой смесь основных солей различного состава и цвета (зеленого и сине-зеленого). Под названием ярь-медянка применяется для приготовления масляной краски.
Комплексные соединения меди образуются в результате соединения двухзарядных ионов меди с молекулами аммиака. Из солей меди получают разноообразные минеральные краски. Все соли меди ядовиты. Поэтому, чтобы избежать образования медных солей, медную посуду покрывают изнутри слоем олова (лудят).
Упругие деформации. Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.
Определение начального модуля упругости бетона в20, в25
Все тела деформируемы
. Изменения, вызванные действиями приложенных сил, при которых тела меняют форму и объем –
деформации
.
Упругие
деформации
– деформации, которые исчезают, после прекращения действия приложенной силы.
Пластические деформации
(
остаточные деформации
) – деформации, которые сохраняются в теле (частично или полностью) после прекращения действия приложенной силы.
Если напряжение
(сила, отнесенная к единице площади) не превышает некоторой величины (
предел упругости
), то деформация будет упругой.
Идеально упругие
тела – тела, которые могут претерпевать только упругие деформации. Для таких тел
существует однозначная зависимость между силами и вызываемыми ими деформациями
.
Малые деформации
– деформации, которые подчиняются
закону Гука
, согласно которому
деформации пропорциональны силам, их вызывающимизотропныеанизотропные
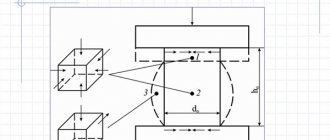
Пусть есть два стержня. Один сжимаем, а другой сдавливаем с силой (как на рисунке). Перпендикулярно к оси стержня проведем сечение . Для равновесия стержня , на его нижнее основание должна действовать сила . Нижняя и верхняя части стержня действуют друг на друга с равной силой , т.к. они деформированы. Отношение силы к площади поперечного сечения – напряжение
.
Натяжение
– напряжение при натяжении, .
Давление
– напряжение при сжатии , где площадь сечения. Давление – отрицательное напряжение и наоборот .
– длина недеформированного стержня. – приращение длины, после приложения силы . Значит полная длина . – относительное удлинение стержня (если – относительное сжатие).
Для малых упругих деформаций натяжение (давление ) пропорционально относительному удлинению (относительному сжатию) —
(),
где – модуль Юнга
(постоянная, зависящая только от материала стержня и его физического состояния).
Модуль Юнга
– натяжение, которое необходимо приложить к стержню, чтобы его длина увеличилась в два раза. А две формулы выше –
закон Гука
.
Вычислим упругую энергию
растянутого стержня. Приложим к стержню растягивающую силу и будем постепенно (непрерывно и медленно) увеличивать ее от до . Удлинение будет меняться от до . По закону Гука ,
где – коэффициент упругости
.
Вся работа по растяжению стержня пойдет на увеличение его упругой энергии . Т.к. в конечном состоянии , то , то для энергии получим .
Под действием растягивающей или сжимающей силы изменяются не только продольные, но и поперечные размеры стержня. Если сила растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются.
– коэффициент Пуассона
.
Он зависит только от материала рассматриваемого тела. Модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства изотропного материала. Все остальные упругие деформации можно выразить через эти коэффициенты.
Post Views: 4 220
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.
Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.
С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости различных материалов
Gsm модуль для котла
Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:
- природы веществ, формирующих состав материала;
- моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
- структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
- плотности материала (распределения частиц в его объеме);
- обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).
Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:
- бронза – 10,4 ГПа;
- алюминиевая бронза при литье – 10,3 ГПа;
- фосфористая бронза катанная – 11,3 ГПа.
Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.
Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:
- литая – 82 ГПа;
- прокатанная – 108 ГПа;
- деформированная – 112 ГПа;
- холоднотянутая – 127 ГПа.
Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.
Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.
Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.
Модули упругости некоторых материалов
На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:
- его диаметр;
- шаг свивки;
- угол свивки.
Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.
Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.
Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.
Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Факторы, влияющие на модуль Юнга
Цены на ограждения из нержавеющей стали за метр
Модуль Юнга – это основная характеристика бетона, определяющая его прочность. Благодаря величине проектировщики проводят расчёты устойчивости материала к различным видам нагрузок. На показатель влияют многие факторы:
- качество и количество заполнителей;
- класс бетона;
- влажность и температура воздуха;
- время воздействия нагрузочных факторов;
- армирование.
ФОТО: dostroy.comМодуль упругости позволяет проектировщикам правильно рассчитывать нагрузку
Качество и количество заполнителей
Качество бетона зависит от его заполнителей. Если компоненты имеют низкую плотность, соответственно, модуль Юнга будет небольшим. Упругость материала возрастает в несколько раз, если применяются тяжёлые наполнители.
ФОТО: russkaya-banja.ruКрупные компоненты увеличивают характеристики упругости
ФОТО: ivdon.ruГрафик зависимости предела прочности материала от цементного камня
Класс материала
На коэффициент влияет и класс бетона: чем он ниже, тем меньше значение модуля упругости. Например:
- модуль упругости у В10 соответствует значению 19;
- В15 – 24;
- В-20 – 27.5;
- В25 – 30;
- показатель у В30 возрастает до значения 32,5.
ФОТО: buildingclub.ruЗависимость от класса бетона
Как влияют на показатель влажность и температурные значения
На рост деформаций и уменьшение упругих свойств материала влияют:
- повышение температуры воздуха;
- увеличение солнечной активности.
Под воздействием негативных факторов окружающей среды внутренняя энергия материала увеличивается, это приводит к линейному расширению бетона и соответственно, к увеличению пластичности.
На ползучесть материала оказывает влажность, приводящая к изменению упругих характеристик. Чем выше содержание водяных паров, тем ниже коэффициент.
ФОТО: betonpro100.ruВлияние влажности на ползучесть бетона
Время воздействия нагрузки и условия твердения смеси
На показатель упругости влияет время воздействия нагрузки:
- при мгновенном усилии на бетонную конструкцию деформативность прямо пропорциональна величине внешней нагрузке;
- при длительном воздействии значения коэффициента уменьшаются.
Во время проведения исследований было отмечено, если бетон твердеет естественным способом, модуль упругости у него выше в отличие от пропаривания материала в различных условиях. Это объясняется тем, что при использовании внешних условий в бетоне образуются пустоты и поры в большом количестве, ухудшающие его упругие свойства.
ФОТО: udarnik.spb.ruЗависимость модулей упругости от разных факторов
Возраст бетона и армирование конструкции
Прочность бетона находится в прямой зависимости от его возраста, со временем показатель только увеличивается. Ещё один фактор, положительно влияющий на модуль упругости бетона, – армирование, которое препятствует деформации материала.
ФОТО: 63-ds.netsamara.ruДля конструкций, которые будут эксплуатироваться под большими нагрузками, необходима укладка металлической решётки
Модуль упругости дерева
Древесина считается упругой, если она после устранения действия силы изгибающей её, принимает исходную форму. У упругости есть предел. Он достигается, когда при изгибе деревянная детальили изделие сохранит конечную форму.Попросту говоря, предел упругости доски достигается в тот момент, когда она ломается. Свойства упругости и гибкости не идентичны. Гибкость – способность менять форму под действием внешних воздействий. Упругость – возможность возвращать утраченную форму. Дерево с высоким модулем необходимо для того, чтобы делать спортивные снаряды, мебель. Наиболее упруга древесина таких пород как ясень, бук, кария, лиственница.
Чтобы описать способность к возвращению исходной формы, используют следующие физические величины:
- модуль упругости Е;
- коэффициент деформации µ;
- модуль сдвига G.
В общем, можно говорить о том, что при приложении силы вдоль древесных волокон, модуль упругости в 20-25 раз выше, чем если та же сила действует поперек волокон. Если сила действует перпендикулярно направлению волокон и направлена радиально, то этот показатель на 20-50 % больше, чем при действии той же силы в тангенциальном направлении.
Ниже рассмотрим более подробно эти физические величины, определяющие способность дерева возвращать исходную форму при снятии деформирующего усилия.
Модуль упругости древесины основных пород
Модуль упругости в физике рассматривается как единое наименование комплекса физических величин, характеризующих способность твердого тела (в нашем случае – дерева) упруго деформироваться, если к нему будет приложена какая-то сила.
Модуль упругости древесины (Е) – соотношение между нормальными напряжениями и относительными деформациями. Он измеряется в Мпа либо в кГс/см2 (1Мпа=10.197 кГс/см2) Выделяют несколько видов:
- вдоль волокон Еа.
- поперек волокон (тангенциальный) Еt.
- поперек волокон (радиальный) Еr.
- модуль упругости при изгибе Еизг.
Таблица. Сведения по наиболее часто используемым породам.*
Коэффициенты поперечной деформации основных пород дерева
Во время приложения нагрузки, кроме продольной деформации вдоль волокон так же появляется поперечная при изгибе.
Коэффициенты этого типа деформации приведены в таблице:
Модуль сдвига основных пород древесины
Модуль сдвига – коэффициент пропорциональности между касательными напряжениями и угловыми деформациями древесины.
Данные по модулю сдвига для основных пород приведены ниже:
Пластичность древесины
Дерево способно под давлением менять без разрушения свою форму, сохранять её после того, как давление будет снято. Такое свойство называется пластичностью. Пластичность зависит от тех же критериев, что упругость, только в обратном направлении. Например, чем выше влажность древесины, тем она более пластична, при этом менее упруга.
Пластичность дерева повышают с помощью специальной обработки. Пропаривая или проваривая его в воде, получаем более пластичный материал, которую затем используют для изготовления мебели, полозьев саней. Наивысшая пластичность у бука, вяза, ясеня, дуба. Это свойство обусловлено строением проводящей системы данных пород. У бука, например, много крупных сердцевинных лучей, изгибающих волокна древесины. Сосуды, расположенные группами в годовых слоях вяза, дуба, ясеня, сильно сдавлены более плотной поздней древесиной, поэтому пластичность этих пород высока.
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
- Fупр — сила упругости
- k × Δl — удлинение тела
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.
Другие формулы вычисления модуля Юнга (модуля упругости)
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
| 1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
| Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Закон Гука в математической форме
Формулировка Гука, которую мы привели выше, дает возможность записать его в следующем виде:
,
где изменение длины тела вследствие сжатия или растяжения, F сила, приложенная к телу и вызывающая деформацию (сила упругости), k коэффициент упругости, измеряется в Н/м.
Следует помнить, что закон Гука справедлив только для малых растяжений.
Также отметим, что он при растяжении и сжатии имеет один и тот же вид. Учитывая, что сила величина векторная и имеет направление, то в случае сжатия, более точной будет такая формула:
, но опять-таки, все зависит от того куда будет направлена ось, относительно которой вы проводите измерение .
В чем кардинальная разница между сжатием и растяжением? Ни в чем, если оно незначительно.
Степень применимости можно рассмотреть в таком виде:
Обратим внимание на график. Как видим, при небольших растяжениях (первая четверть координат) долгое время сила с координатой имеет линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и закон перестает выполняться
На практике это отражается таким сильным растяжением, что пружина перестает возвращаться в исходное положение, теряет свойства. При еще большем растяжении происходит излом, и разрушается структура материала.
При небольших сжатиях (третья четверть координат) долгое время сила с координатой имеет тоже линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и всё вновь перестает выполняться. На практике это отражается таким сильным сжатием, что начинает выделяться тепло и пружина теряет свойства. При еще большем сжатии происходит слипание витков пружины и она начинает деформироваться по вертикали, а затем и вовсе плавиться.
Как видим формула, выражающая закон, позволяет находить силу, зная изменение длины тела, либо, зная силу упругости, измерить изменение длины:
Также, в отдельных случаях можно находить коэффициент упругости. Для того, чтобы понять как это делается, рассмотрим пример задачи:
К пружине подсоединен динамометр. Ее растянули, приложив силу в 20 Ньютон, из-за чего она стала иметь длину 1 метр. Затем ее отпустили, подождали пока прекратятся колебания, и она вернулась к своему нормальному состоянию. В нормальном состоянии ее длина составляла 87, 5 сантиметров. Давайте попробуем узнать, из какого материала сделана пружина.
Дано:
Решение:
Найдем численное значение деформации пружины:
Запишем:
Отсюда можем выразить значение коэффициента:
Посмотрев таблицу, можем обнаружить, что этот показатель соответствует пружинной стали.
Содержание
На все тела, которые находятся на Земле, действует сила тяжести. Все они стремятся под ее действием упасть вниз. Но не похоже, чтобы все в мире лежало на земле.
На еду в вашей тарелке действует сила тяжести, но она же не проваливается сквозь тарелку. На учебник на вашей парте тоже действует сила тяжести. Но стол от этого не придавливается к полу.
Значит, существует некая сила, уравновешивающая силу тяжести. В данном уроке мы узнаем, что же это за сила.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих — повышение предела прочности (селектрон).
Параметры, от которых зависит упругость древесины
Модуль упругости древесины — параметр изменяющийся, на его значение влияют:
- Влажность. Упругость древесины находится в обратной зависимости от влажности. То есть при высокой влажности дерева, его способность возвращаться к исходной форме будет минимальной.
- Прямослойность. Если волокна расположены извилисто, беспорядочно, то способность восстанавливать форму у неё будет заметно ниже, чем у прямослойной.
- Плотность. Дерево с низкой плотностью не так упруго, как более плотное.
- Возраст дерева. Древесина старого дерева более упруга, чем молодого.
- Природные особенности дерева. Хвойные деревья имеют однорядные мелкие сердцевинные лучи, поэтому их древесина более упругая, хотя удельный вес у таких пород не велик.
- Возраст самой древесины. Более молодые слои ствола дерева называют заболонью, те, что располагаются ближе к центру, и, соответственно, старее – ядром. Заболонь более упругая, чем ядро.
Характеристики меди
- Плотность меди — 8,93*103кг/м3;
- Удельный вес меди — 8,93 г/cм3;
- Удельная теплоемкость меди при 20oC — 0,094 кал/град;
- Температура плавления меди — 1083oC ;
- Удельная теплота плавления меди — 42 кал/г;
- Температура кипения меди — 2600oC ;
- Коэффициент линейного расширения меди
- (при температуре около 20oC) — 16,7 *106(1/град);
- Коэффициент теплопроводности меди — 335ккал/м*час*град;
- Удельное сопротивление меди при 20oC — 0,0167 Ом*мм2/м;
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Читать также: Прибор который ищет провода в стене
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
- Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
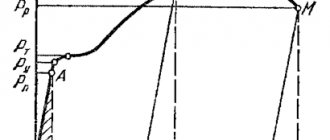
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Модуль упругости фанеры
Фанера – строительный материал, производимый путем склеивания нескольких слоев деревянного шпона. Она очень популяренна, и неспроста. Кроме эстетической ценности, фанера обладает рядом значений параметров, выделяющих её в ряду материалов для строительства. Проходя обработку, фанера приобретает прочность, упругость, влагостойкость.
На характеристики фанеры влияют многие факторы:
- порода дерева, используемого для шпона;
- исходное состояние сырья;
- влажность самой фанеры;
- тип и состав клея, которым соединяются слои шпона;
- технология предварительной обработки.
Для фанеры так же рассчитывается модуль упругости и все соответствующие коэффициенты.
Важно то, что модуль упругости фанеры и другие показатели выше, чем у древесины, из которой она была изготовлена. Модуль упругости древесины рассчитывают обязательно перед постройкой кровельных, стропильных систем
Знание внутренних усилий, появляющихся в строительных материалах, важно для безопасности, долговечности постройки. Способность возвращать утраченную форму значимо при выборе материала рукояток ударных инструментов, оружейных лож
Модуль упругости древесины рассчитывают обязательно перед постройкой кровельных, стропильных систем
Знание внутренних усилий, появляющихся в строительных материалах, важно для безопасности, долговечности постройки. Способность возвращать утраченную форму значимо при выборе материала рукояток ударных инструментов, оружейных лож
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Читать также: Перфоратор макита hr2450 ремонт своими руками
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
- Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
ПОИСК
Е — приведенный модуль Юнга, принятый равным модулю упругости стали [c.71]
Деформационные свойства. Модуль Р. (Е) при небольшом растяжении на 4—5 десятичных порядков ниже модуля Юнга для стали [соответственно 0,5— [c.158]
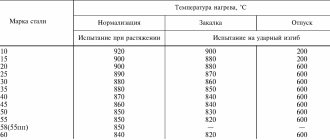
МОДУЛЬ ЮНГА УГЛЕРОДИСТОЙ И ЛЕГИРОВАННОЙ СТАЛЕЙ ПРИ РАЗНЫХ ТЕМПЕРАТУРАХ [c.16]
Следует отметить, что высокая эластичность каучука совершенно отлична от упругих деформаций кристаллических веществ или металлов, составляющих всего несколько процентов от исходных размеров, тогда как каучук можно растягивать в 10 раз.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20000 кг/мм , для стекла около 6000 кг/мм , а для каучука лишь около [c.228]
При конструировании важно установить распределение деформаций конструкции, возникающих в процессе эксплуатации под влиянием приложенных напряжений. Напряжения могут возникать из-за давления, создаваемого жидкостью или газом, течением жидкости или неоднородным температурным расширением при изменениях температуры. Упругие свойства часто считают не зависящими от структуры, но существуют ситуации, когда такое утверждение становится неверным. Отдельные зерна металлических кристаллов в отношении упругих свойств анизотропны. Таким образом, упругие постоянные зависят от ориентации зерна по отношению к ориентации приложенных напряжений. В процессе производства деталей может возникнуть преимущественная ориентация отдельных зерен, что и создает упругую анизотропию. Весьма вероятно, что различные степени преимущественной ориентации приводят к довольно широкому разбросу данных по упругим свойствам металлов и сплавов. Вследствие того что этот разброс может вызывать появление погрешности, достигающей в некоторых случаях при расчетах деформаций 20 %, эта тема детально рассматривается в настоящем параграфе. Таблица 3, 4.5,8 — лишь пример того типа информации, которая встречается в литературе. Можно полагать, например, что стали с 5—9 %-ным содержанием хрома должны иметь примерно те же значения модуля Юнга, что и стали, содержание хрома в которых близко к указанному. [c.196]
Прочность сталей значительно изменяется при переходе к высоким температурам. Так, предел прочности при растяжении хромоникелевой стали типа 18-8 падает с 7000 до 4000 кгс/см при 700 °С до 2000 кгс/см при 800 °С. Модуль Юнга углеродистой и легированной сталей уменьшается при нагревании от 20 до 500 °С на 30%. [c.19]
Иногда для повышения прочности между двумя пьезоэлементами помещают металлическую пластину [318].
Собственная частота преобразователя может быть повышена расположением двух пассивных (например, стальных) пластин по обе стороны от биморфного преобразователя из двух пьезопластин.
Это объясняется тем, что модуль Юнга стали много больше, чем у пьезокерамики, а изгибная жесткость конструкции определяется в основном ее [c.70]
Твердость вещества можно оценить при помощи модуля Юнга, представляющего собой отношение приложенного напряжения (или силы, отнесенной к единице площади) и соответствующей ему деформации или удлинения.
Типичные значения модуля Юнга для различных материалов представлены на рис. 7.1. На одном конце шкалы расположены неорганические кристаллические материалы, такие, как алмаз, кварц, сталь и т. д., модули которых [c.
131]
Еще большее впечатление производит различие в силе, необходимой для осуществления деформации.
Для удлинения стальной проволоки диаметром 1 мм на 1% требуется нагрузка в 1600 Н (двукратный средний вес человека), а для удлинения каучуковой нити того же диаметра на ту же величину необходима нагрузка меньше Ю Н.
Так называемый модуль Юнга (отношение напряжения к удлинению) для стали в 100 000 раз больше, чем для каучука. [c.45]
Характеристика сталей и сплавов при комнатной температуре и частоте колебаний 20 кгц (р — плотность Е — модуль Юнга Спр — скорость звука рс — волновое сопротивление [c.115]
Следует отметить, что для коммуникаций часто применяют титан неоправданно большой толщины, что не вызывается ни прочностными, ни коррозионными требованиями. Часто на титан как конструкционный материал переносятся представления, сложившиеся в результате многолетней работы со сталью.
Так, при замене коммуникаций из стали на титановые используют титан той же толщины, что и сталь. Большой расход титана именно на коммуникации объясняется в некоторой степени и этой причиной.
Например, коллекторы влажного хлора на заводах делают из листов титана толщиной 3—5 мм (только на двух предприятиях эти коллекторы сделаны из листов толщиной 2 мм, но и это значительная толщина). За рубежом для данных целей используют титан толщиной 0,8—1,0 мм.
В связи с тем, что модуль Юнга у титана незначителен, при расчетах следует обращать внимание на возможный прогиб труб, а при монтаже — на крепление трубопроводов. [c.156]
Любопытные наблюдения публикует Фирс-Виккерс, утверждая, что нержавеющие аустенитовые стали (хромовые и хромоникелевые) дают падение модуля Юнга приблизительно на 1% на каждые 30° повыщения температуры. В случае особенно тяжелых условий работы лучше всего обратиться за информацией к поставщикам стали. [c.670]
Вулканизованный каучук способен испытывать обратимые деформации на сотни процентов при весьма малом значении модуля упругости. (Модуль Юнга для стали 20 000—22 000 кг/см , для каучука [c.10]
Следует отметить, что высокая эластичность каучука совершенно отличается от упругих деформаций кристаллических веществ или металлов, которые составляют всего несколько процентов от исходных размеров, тогда как каучук можно растягивать до десятикратных удлинений.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20 ООО кг/мм», для стекла—около 6000 кг/мм , а для каучука—лишь около 0,1 кг/мм». Эти различия объясняются тем, что нри упругой деформации кристаллов происходят лишь небольшие изменения средних расстояний между молекулами и валентных расстояний между атомами, связанные со значительными изменениями внутренней энергии напротив, при чистой высоко-эластической деформации большие удлинения происходят без изменения валентных расстояний нри постоянстве внутренней энергии. [c.272]
На практике все большее применение стали получать ОВ с двуслойным покрытием, в которых первый слой выполнен мягким (буферным) с низким (1—2 МПа) модулем Юнга, а второй—с высоким модулем Юнга от 0,1 до 4 ГПа [52] [c.101]
В формуле (П1.2) за начальную деформацию 5 обычно (но не обязательно) принимается величина некоторой условно упругой деформации, которая определяет начало пластического течения материала.