Why resistance occurs
Electrons, colliding with charged atoms (ions) that make up the crystal lattice of the conductor, lose speed. The mass of an atom significantly exceeds the mass of an electron, so their collision leads to a loss of speed (“braking”) and a change in the direction of motion of the electron. This creates resistance to the flow (increase) of current. This means that resistance is a physical quantity.
Collisions of electrons with atoms.
What is it measured in?
According to the international system of units, the value is measured in ohms multiplied by a meter. In some cases, the unit used is ohm multiplied by millimeter squared divided by meter. This is a designation for a conductor having a meter length and a square millimeter cross-sectional area.
Unit
Dependence of ammeter and voltmeter readings on the conductor used in the circuit
First, let's conduct an interesting experiment. Let's assemble an electrical circuit from a current source, a switch, an ammeter and a voltmeter. We will also include conductors made of various materials in this circuit. They are fixed on a special panel. We will connect a voltmeter in parallel to these same conductors (Figure 1).
Our conductors are designated as follows: AB - iron wire, CD - nickel wire, EF - copper wire.
These conductors have the same length and cross-section.
Figure 1. Dependence of current on the conductor used in the circuit
First we connect the iron wire AB . Let us record the readings of the ammeter and voltmeter after closing the key.
Now let's switch to nickel wire CD . We will notice that the current in the circuit has decreased.
Let's try the third conductor: EF . Now the current has increased significantly .
Have you forgotten that in our experiment there was also a voltmeter? We connected it to each of the conductors in turn.
Each time we got the same voltage value. It didn't change.
Formula how to find
According to the provision from any textbook on electrodynamics, the resistivity of the conductor material formula is equal to the proportion of the total resistance of the conductor per cross-sectional area, divided by the conductor length. It is important to understand that the final indicator will be influenced by temperature and the degree of material purity. For example, if you add a little manganese to copper, the overall indicator will be increased several times.
Main calculation formula
Interestingly, there is a formula for inhomogeneous isotropic material. To do this, you need to know the electric field strength with the electric current density. To find it, you need to divide the first quantity by the other. In this case, the result is not a constant, but a scalar quantity.
Ohm's law in differential form
There is another, more difficult to understand formula for an inhomogeneous anisotropic material. Depends on the tensor coordinate.
It is important to note that the relationship between resistance and conductivity is also expressed by formulas. There are rules for finding isotropic and anisotropic materials through tensor components. They are shown in the diagram below.
Relationship with conductivity expressed in physical relations
What does it depend on
Resistance depends on temperature. It increases when the thermometer rises. This is explained by physicists in such a way that as the temperature increases, atomic vibrations in the crystalline conductor lattice increase. This prevents free electrons from moving around.
Note! As for semiconductors and dielectrics, the value decreases due to the fact that the structure of the concentration of charging carriers increases.
Temperature dependence as the main property of conductive resistance
Dependence of current on the properties of conductors
You already know that current depends on voltage. After all, voltage is a characteristic of the electric field.
But in our experience the tension remained constant. This means that the current strength has another dependence.
The current strength in the circuit depends on the properties of the conductors included in the electrical circuit.
What do resistivity numbers mean?
In order to be able to compare the resistivity of different materials, from products such as copper and aluminum to other metals and substances including bismuth, brass and even semiconductors, it is necessary to use a standard measurement.
The unit of resistivity in the International System of Units (SI) is Ohm m.
The SI unit of resistivity is equal to the resistivity of a substance such that a homogeneous conductor 1 m long with a cross-sectional area of 1 m2, made from this substance, has a resistance of 1 ohm. Accordingly, the resistivity of an arbitrary substance, expressed in SI units, is numerically equal to the resistance of a section of an electrical circuit made of a given substance with a length of 1 m and a cross-sectional area of 1 m2
Resistivity of different materials
It is important to note that the resistance of metal single crystals with metals and alloys is different. Values vary due to chemical metallic purity, formulation methods, and variability. It's also worth keeping in mind that the values change as the temperature changes. Sometimes resistance drops to zero. In this case, the phenomenon is called superconductivity.
It is interesting that under heat treatment, for example, annealing of copper, the value increases 3 times, despite the fact that the proportion of impurities in the durable, anti-corrosion and light composition is, as a rule, no more than 0.1%.
Note! As for the annealing of aluminum, lead or iron, the value under the same conditions increases by 2 times, despite the presence of impurities in the amount of 0.5% and the need for more energy for melting.
Table of composition values at a temperature of 20 degrees Celsius
In general, electrical resistivity is a physical quantity that characterizes the ability of a substance to prevent electric current from passing through. According to SI, it is measured in ohms multiplied by meters. Depends on the increase in temperature of the substance. You can find the value using the formula for the ratio of total resistance and cross-sectional area divided by the length of the conductor. As for the resistivity of alloys, according to the studies of various scientists, their composition is not constant and can be changed by heat treatment.
Resistivity table for common conductors
The table below shows resistivity values for various materials, particularly metals used for electrical conductivity.
Resistivity indicators are given for such “popular” materials as copper, aluminum, nichrome, steel, lead, gold and others.
MaterialResistivity, ρ, at 20 °C (Ohm m)Source
| Brass | ~0.6 – 0.9 x 10-7 | |
| Silver | 1.59×10−8 | [3][4] |
| Copper | 1.68×10−8 | [5][6] |
| Burnt copper | 1.72×10−8 | [7] |
| Gold | 2.44×10−8 | [3] |
| Aluminum | 2.65×10−8 | [3] |
| Calcium | 3.36×10−8 | |
| Tungsten | 5.60×10−8 | [3] |
| Zinc | 5.90×10−8 | |
| Cobalt | 6.24×10−8 | |
| Nickel | 6.99×10−8 | |
| Ruthenium | 7.10×10−8 | |
| Lithium | 9.28×10−8 | |
| Iron | 9.70×10−8 | [3] |
| Platinum | 1.06×10−7 | [3] |
| Tin | 1.09×10−7 | |
| Tantalum | 1.3×10−7 | |
| Gallium | 1.40×10−7 | |
| Niobium | 1.40×10−7 | [8] |
| Carbon steel (1010) | 1.43×10−7 | [9] |
| Lead | 2.20×10−7 | [2][3] |
| Galinstan | 2.89×10−7 | [10] |
| Titanium | 4.20×10−7 | |
| Electrical steel | 4.60×10−7 | [11] |
| Manganin (alloy) | 4.82×10−7 | [2] |
| Constantan (alloy) | 4.90×10−7 | [2] |
| Stainless steel | 6.90×10−7 | |
| Mercury | 9.80×10−7 | [2] |
| Manganese | 1.44×10−6 | |
| Nichrome (alloy) | 1.10×10−6 | [2][3] |
| Carbon (amorphous) | 5×10−4 — 8×10−4 | [3] |
| Carbon (graphite) parallel-basal plane | 2.5×10−6 — 5.0×10−6 | |
| Carbon (graphite) perpendicular-basal plane | 3×10−3 | |
| Gallium arsenide | 10−3 to 108 | |
| Germanium | 4.6×10−1 | [3][4] |
| Sea water | 2.1×10−1 | |
| Swimming pool water | 3.3×10−1 — 4.0×10−1 | |
| Drinking water | 2×101 — 2×103 | |
| Silicon | 2.3×103 | [2][3] |
| Wood (wet) | 103 — 104 | |
| Deionized water | 1.8×105 | |
| Glass | 1011 — 1015 | [3][4] |
| Carbon (diamond) | 1012 | |
| Hard rubber | 1013 | [3] |
| Air | 109 — 1015 | |
| Wood (dry) | 1014 — 1016 | |
| Sulfur | 1015 | [3] |
| Fused quartz | 7.5×1017 | [3] |
| PAT | 1021 | |
| Teflon | 1023 — 1025 |
It can be seen that the resistivity of copper and the resistivity of brass are both low, and considering their cost relative to silver and gold, they become cost-effective materials to use for many wires. Copper's resistivity and ease of use have led to it being widely used as a conductor material on printed circuit boards.
Occasionally, aluminum and especially copper are used due to their low resistivity. Most wires used for interconnection today are made of copper because it provides low resistivity at an affordable cost.
The resistivity of gold is also important because gold is used in some critical applications despite its cost. Gold plating is often found on high quality low current connectors where it provides the lowest contact resistance. The gold coating is very thin, but even so it is able to provide the required characteristics of the connectors.
Silver has a very low level of resistivity, but is not widely used due to its cost and because it tarnishes, which can result in higher contact resistance.
However, it is used in some radio transmitter coils where silver's low electrical resistivity reduces losses. When used for such purposes, silver was usually applied only to the existing copper wire. Coating the wire with silver allowed for significant cost savings compared to solid silver wire without significantly compromising performance.
It will be interesting➡ All about the VVG-Png(A) cable
Other materials in the electrical resistivity table may not have such obvious uses. Tantalum appears in the table because it is used in capacitors—nickel and palladium are used in the end connections of many surface mount components such as capacitors.
Quartz finds its main application as a piezoelectric resonant element. Quartz crystals are used as frequency-determining elements in many oscillators, where the high Q value allows for very frequency-stable circuits. They are similarly used in high efficiency filters. Quartz has a very high level of resistivity and is not a good conductor of electricity, meaning it is classified as a dielectric.
Concept of electrical resistance of a conductor
The classical definition explains electric current by the movement of “free” (valence) electrons. It is provided by the electric field created by the source. Movement in the metal is hampered not only by the normal components of the crystal lattice, but also by defective areas, impurities, and inhomogeneous areas. During collisions with obstacles, due to the transition of momentum into thermal energy, the temperature increases.
A good example is heating water with a boiler.
In gases, electrolytes and other materials the physics of the phenomenon is somewhat different. Linear relationships are observed in metals and other conductors. The basic relationships are expressed by the well-known formula of Ohm's law:
R (electrical resistance) = U (voltage) / I (current).
For convenience, the inverse quantity, conductivity (G = 1/R), is often used. It denotes the ability of a certain material to pass current with certain losses.
To simplify, the example of a water pipe is sometimes used. A moving fluid is an analogue of a current. Pressure is the equivalent of voltage. By decreasing (increasing) the cross section or position of the locking device, the conditions of movement are determined. In a similar way, the basic parameters of electrical circuits are changed using resistance (R).
For your information. The amount of liquid passing per unit time through the control section of the pipe is the equivalent of electrical power.
The reciprocal of resistivity is called electrical conductivity.
c = 1/r = l
/SR = a with z (l+ + l-)
Dimension of specific electrical conductivity Ohm-1 m-1 = S/m (S – Siemens)
The specific electrical conductivity of a solution characterizes the electrical conductivity of a volume of solution enclosed between two parallel electrodes having an area of 1 m2 and located at a distance of 1 m from each other.
Equivalent electrical conductivity
.
To highlight the effects of ion-ion interaction, the electrical conductivity c is divided by z + n + c, or zn-c, where c is
the number of moles per unit volume:
l = c/z+n+с = c/zn-с
(z+n+c = zn-c is the number of gram equivalents per unit volume, g-eq/m3)
The quantity l is called equivalent electrical conductivity . li [m2 Ohm-1/g-eq].
It represents the electrical conductivity of a volume of electrolyte containing 1 g-equiv of a dissolved substance and located between two parallel electrodes at a distance of 1 m from each other. The dimension of the equivalent electrical conductivity is m2 Ohm-1 = m2 Sm, then the concentration should be expressed in mol/m3.
For a binary electrolyte l = c/zс = a с z (l+ + l-)/zc = a (l+ + l-)
In solutions of strong electrolytes, for which a®1 l = l+ + l-
For infinite dilution a®1, then l0 = l+0 + l-0
According to Arrhenius theory l = a l0
U = Er + Eom + Djк + Djа ; Eohm=IR
Equilibrium electrode potential. Nernst level. Standard electrode potential
The onset of equilibrium between Me and its salt solution is characterized by the fact that a certain value is established. in magnitude and direction of potential jumps or equilibrium potential. (measure of change in Gibbs energy)
Equilibrium prevents further oxidation and reduction, so the equilibrium potential can serve as a measure of maxims. work of a process that strives to complete. on the electrode.
Me speeds level out
i=i=iº — exchange current
- does not depend on the activity of the participants in the process, but is defined.
only the nature of the electrode and solution. (a = 1). Values can be measured on the basis of TD data, is a constant. If negative, then the metal will be oxide with hydrogen. If positive, then it will not oxidize.
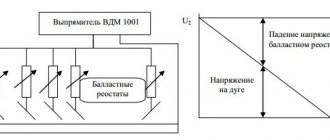
Polarization curves under conditions of electrochemical overvoltage
Calculated using the f-let polarization curve, the symmetry relative to the origin of coordinates is broken when deviating from 0.5. The dotted line shows the polarization curves corresponding to the dependence of the partial current densities in forward and reverse on the potential.
h = a + b log i- Tafel equation. The values of i0 and a can be found graphically (Fig.) by plotting h against log i in the overvoltage region where the Tafel equation is valid. The slope b of the straight line h - log i is equal to
and therefore
The exchange current can be determined by the magnitude of the overvoltage at unit current density, that is, at lg i = 0. Then h=a
Rice.
Determination of Tafel constants a
and
b
from semilogarithmic dependences of overvoltage on current density
Ticket
1 diffusion in solutions of electrolytes. A change in the concentration (or rather activity) of a dissolved substance in one part of the solution relative to another leads to the emergence of a diffusion flow.
The quantitative expression of diffusion processes is Fick's laws. Fick's first law relates to stationary diffusion processes and has the form
jd = -Di grad ci jd+ = -D+ dc+/dx
diffusion flux, that is, the number of particles diffusing through a unit area per unit time. Di is the diffusion coefficient of particles i, has the dimension m2/s, shows the number of particles that diffused in 1 s through a cross section of a solution with an area of 1 m2 with a concentration gradient equal to unity.
Ion diffusion coefficients are related to ion mobilities as follows
jd = -Deff grad c
In general, the mobilities of cations and anions are not the same
l+0 ¹ l-0
and therefore their diffusion coefficients D+ ¹ D- are not equal, therefore, at the same concentration gradient, the diffusion rates of positive and negative ions are different.
Let's assume that a boundary is created between two solutions with different concentrations. For example, NaCl solution.
Let c1>c2. In an aqueous solution of NaCl D+ < D-. Under this condition, anions at the initial moment of time will move from left to right (с1 ®с2) faster than cations. As a result of this, a spatial separation of charges will occur and an electric field will arise, which will accelerate the movement of cations and slow down the movement of anions. Consequently, after a short period of time, the rates of movement of cations and anions will level out. Under these conditions, we can talk about the total flow of electrolyte. However, this flow is not an ordinary diffusion flow, since a stationary potential difference is established between two areas of the solution with concentrations c1 and c2, which is called the diffusion potential jd.
is the effective diffusion coefficient of the electrolyte. The term effective reflects the fact that in reality the movement of ions occurs not only due to diffusion, but also under the influence of an electric field (migration).
The magnitude of the diffusion potential will be determined by the relation
2. The speed of an electrochemical reaction An electrochemical reaction can be considered as a heterogeneous chemical reaction and its speed, like the speed of any chemical reaction, is defined as the amount of substance that changes per unit time, that is
V = ± dDm/dt
Since there is a direct proportionality between the amount of reacted substance and the amount of electricity, according to Faraday’s law, we can write
V = ± dDm/dt = k I dt/dt = k I
The rate of the electrochemical reaction is proportional to the current. A characteristic feature of all electrochemical reactions is that they occur at the electrode-electrolyte interface and therefore their speed depends on the size of the interface. i
= I/S – current density [A/cm2].
If the electrochemical circuit works like an electrolyzer, then
U = Er + Djк + Dja + Eоm,
and if - as a chemical source of current, then
U = Er - Djк - Dja - Eом
electrode polarization (Dj) can be defined, that is, as the difference between the potential of the electrode through which current flows (ji) and its equilibrium potential (jr)
Dj = ji - jr
Any electrode process always has a number of successive stages: first, the reactant approaches the electrode, then the electrochemical stage itself occurs, associated with the transfer of electrons or ions across the phase boundary (discharge -ionization stage
), and finally, the resulting reaction products must move away from the electrode surface.
The first and third stages have the same patterns and are called mass transfer stages
.
The stages of mass transfer and discharge-ionization are present in all electrode processes without exception. In addition to these stages, others also occur during electrode reactions. Thus, electrode processes can be complicated by chemical reactions in the bulk of the solution or on the surface of the electrode, in which the starting substance or the product of the electrochemical reaction may participate. The speed of a process consisting of a number of successive stages is determined by the speed of the slowest stage, which is called limiting
or
controlling
. If the nature of the limiting stage is known, then polarization is replaced by overvoltage. types:
Diffusion overvoltage occurs during the limiting stage of mass transfer;
· Electrochemical overvoltage (discharge-ionization) occurs during the limiting stage of the discharge - ionization;
· Phase overvoltage occurs during the limiting stage of construction or destruction of the crystal lattice or the nucleation of a new phase (gas, liquid, crystalline);
· Chemical reaction overvoltage occurs when the chemical reaction stage is slow.
3 chemical chains with individual molten salts and salt mixtures. In chemical circuits, the current-generating process is associated with the interaction of pure components and the formation of the corresponding salt.
1) With ind. Molten salt
This is a circuit with one salt as an electrolyte, in which electrodes are placed: metal and gas.
Pb|PbCl2|Cl2,C
E measurement will correspond to the standard value
A DEL is formed at the interface and a potential jump occurs. Gas electrodes have more + φ than metal electrodes, therefore a difference φ arises, and in the EMF system
DG0 = - zFE0
DS0 = zF
DH0 = DG0 + TDS0 = - zFE0 + zFT.
2) Chemical chains with molten salt mixtures
Pb|PbCl2, LiCl|Cl2,C; Ag|AgI, KI|I2,C
A solution of t/c Pb is more electropositive, LiCl is a background, independent electrolyte.
The current-generating process is the formation of MeX2 (PbCl2, AgI) from pure metal and halogen.
Ticket
1. jumps in potential at the phase boundary. The electrode potential is the EMF of an electrochemical circuit in which there is a standard hydrogen electrode on the left, the potential of which is conventionally taken to be zero, and this electrode is on the right.
| M1 |
| L1 |
| L2 |
| M2 |
| M1 |
| HER |
E is the total effect of potential jumps at the interfaces
= mia ± ziFga; – electrochemical potential of particles of type i in phase a; ga – internal potential , which is the potential difference between a point inside phase a and an infinitely distant point in vacuum; zi is the charge of particles of type i. The equilibrium condition for charged particles with phases a and b will be the equality of their electrochemical potentials. =
The work of transferring a charged particle from phase a to phase b will be equal to the difference in its electrochemical potentials in these phases, that is - = (mia - mib) ± ziF(ga - gb)
The electrochemical potential of particle i in phase a is equal to the work of transferring a mole of a given component i from infinity in a vacuum into a given phase.
ga - gb - the difference in internal potentials is called the galvanic potential and is denoted as gab. Under equilibrium conditions gab = (mia - mib)/ ziF the EMF of the electrochemical system, which is the sum of potential jumps at the phase boundaries, is at the same time the sum of all galvanic potentials. E = gM1L1 + gL1L2 + gL2M2 + gM2M1
If there is no potential gL1L2 in the electrochemical system, then E = gM1L1 - g M2L2 - gM1M2
On the other hand, EMF is the difference between two electrode potentials, that is
E = jп - jл
2. Concentration electrochemical. circuits Both electrodes are identical in physical state and chemical nature. They differ in the concentration of Ox and Red components.
The source of electrical energy is the difference in Gibbs free energies, caused by different activities of the same chemical components.
Concentration chains can be prepared as follows:
1. From amalgams of different concentrations in the same solution;
2. From identical electrodes of the 1st and 2nd kind, located in solutions of different concentrations (activities);
3. From identical gas electrodes operating at different pressures.
There are concentration chains without transfer and with transfer. When concentration chains operate, activities or pressures are equalized. Cu çZn (Hg)(a1) ç ZnSO4 ç Zn (Hg)(a2) çCu chain without transfer
If a1 > a2, then the left electrode is the anode, and the right electrode is the cathode.
E = jк - jа = RT/2F ln a1/a2Zn ç ZnSO4 (a')çç ZnSO4 (a'')ç Zn transfer circuit
If a' < a'', then the left electrode is the anode, and the right electrode is the cathode. E = jк - ja = RT/2F ln a''/a' K: Cu2++2e=Cu0 A: Cu0-2e=Cu2+
3. Electrolysis of molten salts is widely used to produce light, refractory, rare metals, alloys, fluorine, chlorine, and for metal refining. The use of electrolysis of molten salts is very promising for the production of alloys and compounds, as well as for electroplating and surface treatment of metals.
· high intensity of the process, which can be 25-100 times higher than the intensity of electrolysis of aqueous solutions;
· ability to work in a wide range of temperatures and electrolyte concentrations; significant reduction in water consumption.
· significant specific energy consumption,
· increased capital and operating costs for environmental protection,
It is currently believed that molten salts are close in structure to solid matter. Molten salts at temperatures close to the melting point inherit the structure of the solid substance. The structure of a solid crystal is characterized by long-range order, i.e. the correct arrangement of particles one next to the other throughout the entire volume of the crystal. But there are various defects. They move away with an increase in temperature, thereby reducing the long-range order. When changing into a liquid state, the long-range order is completely destroyed, but matures short-range order. A number of salts have a molecular structure; when they are heated, the structure is retained and the melt becomes non-conducting. Some salts are characterized by a layered structure, in this case the crystal consists of separate packets.
Ticket
1. DES When two phases containing charged particles come into contact, a transition of such particles in unequivalent quantities from phase to phase is possible. In this case, electric charges arise in the surface layers of each phase, equal in magnitude but opposite in sign. A so-called electric double layer (DEL) is formed, the charge difference between the plates of which causes a potential jump.
An example is the interface between a metal and an aqueous electrolyte solution.
EDL can be formed without the transition of charged particles from phase to phase. In this case, the formation of DES is possible due to the selective adsorption of ions of one of the phases on the surface of the other. DES can be formed by the adsorption and orientation of polar molecules of the liquid phase (for example, water) on the surface of a solid.
Me Mez+ + ze (A) oxidation
Me Mez+ + ze (B) reduction
The speeds of the forward and reverse processes are not the same
The rate of reduction and oxidation can be measured by current density
reaction A i
reaction B
i
As these charges increase, the rate of reaction B will decrease and the rate of reaction A will increase until equilibrium is reached
Temperature dependence ρ(T)
For most materials, numerous experiments have been carried out to measure resistivity values. Data for most conductors can be found in reference tables.
Specific resistance of metals and alloys, Ohm*mm2/m
(at T = 20C)
| Silver | 0,016 | Bronze (alloy) | 0,1 |
| Copper | 0,017 | Tin | 0,12 |
| Gold | 0,024 | Steel (alloy) | 0,12 |
| Aluminum | 0,028 | Lead | 0,21 |
| Iridium | 0,047 | Nickelin (alloy) | 0,42 |
| Molybdenum | 0,054 | Manganin (alloy) | 0,45 |
| Tungsten | 0,055 | Constantan (alloy) | 0,48 |
| Zinc | 0,06 | Titanium | 0,58 |
| Brass (alloy) | 0,071 | Mercury | 0,958 |
| Nickel | 0,087 | Nichrome (alloy) | 1,1 |
| Platinum | 0,1 | Bismuth | 1,2 |
Most often, the values of ρ are given at normal, that is, room temperature 20C. But it turned out that with increasing temperature, the resistivity increases linearly in accordance with the formula:
$ ρ(T) = ρ0 * (1 + α*T)$ (6),
where: ρ is the resistivity of the conductor at a temperature of 0C, α is the temperature coefficient of resistivity, which also has its own individual meaning for each substance. From formula (6) it follows that the coefficient α has dimension or .
In accordance with the Joule-Lenz law, when an electric current flows, heat is released, which means the temperature of the conductor increases. In addition, depending on the area of application, electrical devices can operate at both low (minus) and high temperatures. For accurate calculations of electrical circuits, it is necessary to take into account the dependence ρ(T). The value of α for a specific material can be found in reference literature.
Use of substances for the manufacture of conductors and isolates
Which substances have the highest resistivity values? Of course, with dielectrics. For example, ebonite and porcelain practically do not conduct electricity. That's why they are used as insulators .
Pure metals have the lowest resistivity. Silver and copper are the best conductors of electricity.
What substances are conductors used in practice made from? Most often, copper, aluminum and iron wires are used for wiring electrical circuits.
In Table 1, you may also have noticed the resistivity values for alloys of several substances. They have quite large values. For what? They are usually used for the manufacture of devices that need to have a high resistance for normal functioning, but still pass current.
Electrical resistivity
Further research made it possible to establish a connection between the value of electrical resistance and its basic geometric dimensions. It turned out that the resistance of the conductor is directly proportional to the length of the conductor L and inversely proportional to the cross-sectional area of the conductor S.
This functional relationship is well described by the following formula:
$ R = ρ *{ Lover S} $ (4)
The constant value ρ for each substance was called resistivity. The value of this parameter depends on the density of the substance, its crystal structure, atomic structure and other internal characteristics of the substance. From formula (4) you can obtain a formula for calculating resistivity if experimental values for R, L and S are available:
$ ρ = R*{ Sover L } $ (5)
For most known substances, measurements were made and entered into reference tables of electrical resistance of conductors.
Specific resistance of metals, Ohm*mm2/m
(at T = 20C)
| Silver | 0,016 | Bronze (alloy) | 0,1 |
| Copper | 0,017 | Tin | 0,12 |
| Gold | 0,024 | Steel (alloy) | 0,12 |
| Aluminum | 0,028 | Lead | 0,21 |
| Iridium | 0,047 | Nickelin (alloy) | 0,42 |
| Molybdenum | 0,054 | Manganin (alloy) | 0,45 |
| Tungsten | 0,055 | Constantan (alloy) | 0,48 |
| Zinc | 0,06 | Titanium | 0,58 |
| Brass (alloy) | 0,071 | Mercury | 0,958 |
| Nickel | 0,087 | Nichrome (alloy) | 1,1 |
| Platinum | 0,1 | Bismuth | 1,2 |
It was experimentally discovered that as the temperature decreases, the resistance of metals decreases. When approaching the temperature of absolute zero, which is -273C, the resistance of some metals tends to zero. This phenomenon is called superconductivity. Atoms and molecules seem to “froze”, stop any movement and offer no resistance to the flow of electrons.
Iron as a conductor in electrical engineering
Iron is the most common metal in nature and technology (after hydrogen, which is also a metal). It is the cheapest and has excellent strength characteristics, therefore it is used everywhere as the basis for the strength of various structures.
In electrical engineering, iron is used as a conductor in the form of flexible steel wires where physical strength and flexibility are needed, and the required resistance can be achieved through the appropriate cross-section.
Having a table of resistivities of various metals and alloys, you can calculate the cross-sections of wires made from different conductors.
As an example, let's try to find the electrically equivalent cross-section of conductors made of different materials: copper, tungsten, nickel and iron wire. Let's take aluminum wire with a cross-section of 2.5 mm as the initial one.
We need that over a length of 1 m the resistance of the wire made of all these metals is equal to the resistance of the original one. The resistance of aluminum per 1 m length and 2.5 mm section will be equal to
, where R is the resistance, ρ is the resistivity of the metal from the table, S is the cross-sectional area, L is the length.
Substituting the original values, we get the resistance of a meter-long piece of aluminum wire in ohms.
After this, let us solve the formula for S
, we will substitute the values from the table and obtain the cross-sectional areas for different metals.
So,
Since the resistivity in the table is measured on a wire 1 m long, in microohms per 1 mm2 section, then we got it in microohms. To get it in ohms, you need to multiply the value by 10-6. But we don’t necessarily need to get the number ohm with 6 zeros after the decimal point, since we still find the final result in mm2.
- Copper
- Tungsten
- Nikelin
- Iron
As you can see, the resistance of the iron is quite high, the wire is thick.
It will be interesting➡ Twisted pair: categories, crimping, work tips
But there are materials for which it is even greater, for example, nickel or constantan.
Experimental results
What conclusions can we draw after all the calculations?
- Of two nickel wires of the same thickness, longer wire has greater resistance.
- The nickel wire with a smaller cross-section a greater resistance . In this case, the length of the wires was the same
- Nickelin and nichrome wires have different resistances with the same dimensions
Why do metals have the lowest resistivities?
From the table above it can be seen that metals have the lowest resistivity values: silver, copper, gold, aluminum, etc. This property of metals is associated with a high concentration of free electrons, “not tied” to a specific atom, but wandering in the space of the crystal lattice. Voltage applied to the ends of a conductor creates an electric field that acts on the electrons, causing them to move in concert in the same direction.
Rice. 2. Electric current in metals, free electrons.
Silver has the lowest ρ value - 0.016 Ohm*mm2/m. But for widespread, mass use in power supply networks and equipment, this metal is not used due to its too high price. Silver is used to create the most critical contacts in special electrical devices. The following table shows the resistivity values of metals and alloys, commonly used metals in electrical engineering:
Table
Specific resistances of metals, Ohm*mm2/m
(at T = 200C)
| Silver | 0,016 | Bronze (alloy) | 0,1 |
| Copper | 0,017 | Tin | 0,12 |
| Gold | 0,024 | Steel (alloy) | 0,12 |
| Aluminum | 0,028 | Lead | 0,21 |
| Iridium | 0,047 | Nickelin (alloy) | 0,42 |
| Molybdenum | 0,054 | Manganin (alloy) | 0,45 |
| Tungsten | 0,055 | Constantan (alloy) | 0,48 |
| Zinc | 0,06 | Titanium | 0,58 |
| Brass (alloy) | 0,071 | Mercury | 0,958 |
| Nickel | 0,087 | Nichrome (alloy) | 1,1 |
| Platinum | 0,1 | Bismuth | 1,2 |
The most popular in electrical engineering are copper and aluminum. Copper and copper alloys are used to make cable products and shunts - parts that limit large currents through measuring instruments.
Use in electrical engineering
Changing a parameter at different temperatures is widely used in electrical engineering. The simplest example is an incandescent lamp, which uses a nichrome filament. When heated, it begins to glow. When current passes through it, it begins to heat up. As heating increases, resistance also increases. Accordingly, the initial current that was needed to obtain lighting is limited. A nichrome spiral, using the same principle, can become a regulator on various devices.
Precious metals, which have suitable characteristics for electrical engineering, are also widely used. For critical circuits that require high speed, silver contacts are selected. They are expensive, but given the relatively small amount of materials, their use is quite justified. Copper is inferior to silver in conductivity, but has a more affordable price, which is why it is more often used to create wires.
In conditions where extremely low temperatures can be used, superconductors are used. For room temperature and outdoor use they are not always appropriate, since as the temperature rises their conductivity will begin to fall, so for such conditions aluminum, copper and silver remain the leaders.
In practice, many parameters are taken into account and this is one of the most important. All calculations are carried out at the design stage, for which reference materials are used.
Effect of temperature on resistivity
In reference books, the values of ρ of metals are given at room temperature 200C. But experiments have shown that the dependence ρ(T) is linear and is described by the formula:
$ ρ(T) = ρ0 * (1 + α*T)$ (3),
where: ρ0 is the resistivity of the conductor at a temperature of 00C, α is the temperature coefficient of resistance, which is also individual for each substance. Values of α obtained experimentally can be found in reference books. Below are α values for some metals:
- Silver - 0.0035;
- Copper - 0.004;
- Aluminum - 0.004;
- Iron - 0.0066;
- Platinum - 0.0032;
- Tungsten - 0.0045.
Thus, as the temperature increases, the resistance of metals increases. This is explained by the fact that with increasing temperature, the number of defects in the crystal lattice increases due to more intense thermal vibrations of the ions, which inhibit the electron current.
Temperature dependence of resistivity of metals.
As the metal temperature approaches absolute zero, the resistivity drops sharply to zero. This phenomenon is called superconductivity, and materials that exhibit this ability are called superconductors. This effect was discovered in 1911 by the Dutch physicist Kamerlingh Onnes. In his experiment, the resistivity of mercury decreased to zero at 4.10K.
What formula can be used to calculate the resistance of conductors?
Using the new value, we can now calculate the resistance of any conductor.
$R = \frac{\rho l}{S}$, where $\rho$ is the resistivity of the conductor, $l$ is the length of the conductor, $S$ is its cross-sectional area.
From this calculation formula we can express other quantities:
$l = \frac{RS}{\rho}$, $S = \frac{\rho l}{R}$, $\rho = \frac{RS}{l}$.
Properties of resistive materials
The resistivity of a metal depends on temperature. Their values are usually given for room temperature (20°C). The change in resistivity as a result of a change in temperature is characterized by a temperature coefficient.
For example, thermistors (thermistors) use this property to measure temperature. On the other hand, in precision electronics, this is a rather undesirable effect. Metal film resistors have excellent temperature stability properties. This is achieved not only due to the low resistivity of the material, but also due to the mechanical design of the resistor itself.
Many different materials and alloys are used in the manufacture of resistors. Nichrome (an alloy of nickel and chromium), due to its high resistivity and resistance to oxidation at high temperatures, is often used as a material for making wirewound resistors. Its disadvantage is that it cannot be soldered. Constantan, another popular material, is easy to solder and has a lower temperature coefficient.
Content
Ohm's law for a section of a chain connects three quantities: $I = \frac{U}{R}$. These quantities are: current, voltage and resistance. The current strength in the conductor and the voltage at its ends can vary. They are directly proportional to each other. You also know that the current strength in a conductor and resistance are related to each other by inverse proportionality.
But the fact is that electrical resistance is a constant value in Ohm’s law. It does not change when current or voltage changes. Resistance depends solely on the properties of the conductor.
In this lesson we will look at what properties of a conductor its resistance depends on, introduce the concept of “ resistivity ” and compare its values for different substances.
High conductivity materials
The most widespread materials of high conductivity include copper and aluminum (Superconducting materials, which have a typical resistance 10-20 times lower than ordinary conductive materials (metals), are discussed in the section Superconductivity).
Copper
The advantages of copper, which ensure its widespread use as a conductor material, are as follows:
- low resistivity;
- sufficiently high mechanical strength;
- corrosion resistance is satisfactory in most applications;
- good workability: copper is rolled into sheets, strips and drawn into wire, the thickness of which can be increased to thousandths of a millimeter;
- relative ease of soldering and welding.
Copper is most often obtained by processing sulfide ores. After a series of ore smelting and roasting with intense blasting, copper intended for electrical purposes must undergo a process of electrolytic purification.
Copper grades M1 and M0 are most often used as conductor material. M1 grade copper contains 99.9% Cu, and in the total amount of impurities (0.1%) oxygen should be no more than 0.08%. The presence of oxygen in copper worsens its mechanical properties. The best mechanical properties are found in M0 grade copper, which contains no more than 0.05% impurities, including no more than 0.02% oxygen.
Copper is a relatively expensive and scarce material, so it is increasingly being replaced by other metals, especially aluminum.
In some cases, alloys of copper with tin, silicon, phosphorus, beryllium, chromium, magnesium, and cadmium are used. Such alloys, called bronzes, with the correct composition, have significantly higher mechanical properties than pure copper.
Aluminum
Aluminum is the second most important conductor material after copper. This is the most important representative of the so-called light metals: the density of cast aluminum is about 2.6, and rolled aluminum is 2.7 Mg/m3. Thus, aluminum is approximately 3.5 times lighter than copper. The temperature coefficient of expansion, specific heat capacity and heat of fusion of aluminum are greater than those of copper. Due to the high values of specific heat capacity and heat of fusion, heating aluminum to the melting point and transferring it to a molten state requires more heat than heating and melting the same amount of copper, although the melting point of aluminum is lower than that of copper.
Aluminum has lower properties compared to copper - both mechanical and electrical. With the same cross-section and length, the electrical resistance of an aluminum wire is 1.63 times greater than that of a copper wire. It is very important that aluminum is less scarce than copper.
For electrical purposes, aluminum containing no more than 0.5% impurities, grade A1, is used. Even purer AB00 grade aluminum (no more than 0.03% impurities) is used for the manufacture of aluminum foil, electrodes and housings of electrolytic capacitors. Aluminum of the highest purity AB0000 has an impurity content of no more than 0.004%. Additives of Ni, Si, Zn or Fe at a content of 0.5% reduce the γ of annealed aluminum by no more than 2-3%. A more noticeable effect is exerted by Cu, Ag and Mg impurities, which, at the same mass content, reduce γ aluminum by 5-10%. Ti and Mn greatly reduce the electrical conductivity of aluminum.
Aluminum oxidizes very actively and becomes covered with a thin oxide film with high electrical resistance. This film protects the metal from further corrosion.
It will be interesting➡ Capacitor energy
Aluminum alloys have increased mechanical strength. An example of such an alloy is Aldrey, containing 0.3-0.5% Mg, 0.4-0.7% Si and 0.2-0.3% Fe. In aldrey, the Mg2Si compound is formed, which imparts high mechanical properties to the alloy.
Iron and steel
Iron (steel), as the cheapest and most accessible metal, which also has high mechanical strength, is of great interest for use as a conductor material. However, even pure iron has a significantly higher resistivity compared to copper and aluminum; ρ steel, i.e. iron mixed with carbon and other elements is even higher. Ordinary steel has low corrosion resistance: even at normal temperatures, especially in conditions of high humidity, it quickly rusts; As the temperature rises, the corrosion rate increases sharply. Therefore, the surface of steel wires must be protected by a layer of more resistant material. Zinc coating is usually used for this purpose.
In some cases, to reduce the consumption of non-ferrous metals, the so-called bimetal is used. It is steel coated on the outside with a layer of copper, with both metals connected to each other firmly and continuously.
Sodium
Sodium metal is a very promising conductor material. Sodium can be obtained by electrolysis of molten sodium chloride NaCl in virtually unlimited quantities. From a comparison of the properties of sodium with the properties of other conductor metals, it is clear that the resistivity of sodium is approximately 2.8 times greater than ρ of copper and 1.7 times greater than ρ of aluminum, but due to the extremely low density of sodium (its density is almost 9 times less than the density of copper), a wire made of sodium for a given conductivity per unit length should be significantly lighter than a wire made of any other metal. However, sodium is extremely active chemically (it oxidizes intensely in air and reacts violently with water), which is why the sodium wire must be protected with a sealing sheath. The sheath must give the wire the necessary mechanical strength, since sodium is very soft and has a low tensile strength during deformation.
Production technology
To obtain a superconductor, a conductive layer consisting of an alloy of nickel and copper is applied to a copper wire in a vacuum along its entire perimeter, with diffusion into the surface layer of the base wire. A protective layer of metal is applied to the outside. After which the resulting wire is annealed in a vacuum for 30 - 180 minutes at 850-950 o C. To create a copper-nickel wire, pure (99.99) copper and nickel are used.
The effect of increased conductivity is formed in an alloy layer consisting of two metals, which is a thin-walled conductive tube-interlayer. Thanks to the diffusion interaction of the metal layers adjacent to the interlayer tube on both sides, the surface is almost ideal.
The application of wire layers occurs in vacuum equipment to prevent oxidation of the conductive layer. Therefore, the length depends on the capabilities of the vacuum equipment.
What is the resistance of copper wire
In metals, a current is formed when an electric field appears. It “forces” electrons to move in an orderly manner, in one direction. Electrons from the distant orbits of an atom, weakly held by the nucleus, form a current.
Copper wires
As negative particles pass through the crystal lattice of copper molecules, they collide with atoms and other electrons. There is an obstacle or resistance to the directional movement of particles.
To evaluate the resistance to current, the value of “electrical resistance” or “electrical impedance” was introduced. It is designated by the letter “R” or “r”. Resistance is calculated using Georg Ohm's formula: R=, where U is the potential difference or voltage acting on a section of the circuit, I is the current strength.
Concept of resistance
Important! The higher the impedance value of a metal, the less current passes through it, and it is copper conductors that are so widespread in electrical engineering due to this property.
Based on Ohm's formula, the magnitude of the current is affected by the applied voltage at a constant R. But the resistance of copper wires varies depending on their physical characteristics and operating conditions.
The concept of resistance is clear
This is a quantity that determines the ability of a semiconductor element to pass electric current through itself. A general concept can be given based on the basic structure of metals. A metal consists of a crystal lattice, between the elements of which electrons travel. The external field will cause them to create an electric current when moving. The lattice allows them to move through a given volume, and the electrons will rub against its nodes and will not be able to squeeze through. This phenomenon is called resistance, namely: a force that will interfere with movement.
It can be even easier to imagine using a strainer on the sink. The water will move slower than it would without it.
@yaklass.ru
What affects the resistance of a copper wire
The electrical impedance of a copper cable depends on several factors:
- Specific resistance;
- Wire cross-sectional area;
- Wire lengths;
- External temperature.
The last point can be neglected in conditions of domestic use of the cable. A noticeable change in impedance occurs at temperatures above 100°C.
Resistance dependence
Resistivity in the SI system is denoted by the letter ρ. It is defined as the resistance value of a conductor having a cross-section of 1 m2 and a length of 1 m, measured in Ohm ∙ m2. This dimension is inconvenient in electrical calculations, so the unit of measurement Ohm ∙ mm2 is often used.
Important! This parameter is a characteristic of the substance - copper. It does not depend on the shape or cross-sectional area. The purity of the copper, the presence of impurities, the method of making the wire, and the temperature of the conductor are factors that affect the resistivity.
The dependence of the parameter on temperature is described by the following formula: ρt= ρ20[1+ α(t−20°C)]. Here ρ20 is the resistivity of copper at 20°C, α is an empirically found coefficient, from 0°C to 100°C for copper it has a value equal to 0.004 °C-1, t is the temperature of the conductor.
Below is a table of ρ values for different metals at a temperature of 20°C.
Resistivity table
According to the table, copper has a low resistivity, lower only for silver. This ensures good conductivity of the metal.
The thicker the wire, the lower its resistance. The dependence of R of the conductor on the cross-section is called “inversely proportional”.
Important! As the cross-sectional area of the cable increases, it is easier for electrons to pass through the crystal lattice. Therefore, with increasing load and increasing current density, the cross-sectional area should be increased.
An increase in the length of a copper cable entails an increase in its resistance. Impedance is directly proportional to the length of the wire. The longer the conductor, the more atoms there are in the path of free electrons.
conclusions
The last element that affects the resistance of copper is the temperature of the environment. The higher it is, the greater the amplitude of movement of the atoms of the crystal lattice. Thus, they create an additional obstacle for electrons participating in directed movement.
Important! If you lower the temperature to absolute zero, which has a value of 0° K or -273°C, then the opposite effect will be observed - the phenomenon of superconductivity. In this state, the substance has zero resistance.
Temperature correlation
Comparison of conductivity of different types of steel
The characteristics of steel depend on its composition and temperature:
- For carbon alloys, the resistance is quite low: it is 0.13-0.2 μOhm/m. The higher the temperature, the greater the value;
- Low-alloy alloys have a higher resistance - 0.2-0.43 μOhm/m;
- High-alloy steels have high resistance - 0.3-0.86 μOhm/m;
- Due to the high chromium content, the resistance of chromium stainless alloys is 0.5-0.6 μOhm/m;
- Chromium-nickel austenitic steels are stainless and, thanks to nickel, have a high resistance of 0.7-0.9 μOhm/m.
Copper ranks second in terms of electrical conductivity: it perfectly passes electric current and is widely used in the manufacture of wires. Aluminum is also used no less often: it is weaker than copper, but cheaper and lighter.
Active resistance of wires, cables and lines
Due to the fact that alternating current flows unevenly, under the same conditions, alternating and direct current R will be different. As already mentioned, steel electrical wires have a better active R compared to conductors made of non-ferrous metals, which have the same R at any current strength.
On the contrary, the active R of steel electrical cables always depends on the electric current, so DC conductivity is never used in this case. The active R of an electrical cable is determined using the formula: R=l/y*s.
What it is
The resistivity of a conductor is a physical quantity that indicates that a material can resist electric current. In other words, this is the resistance of metals that a material with a unit cross section provides resistance to flowing current. DC resistivity differs in that it is caused by current flowing into the conductor. As for alternating current, it appears in a conductor under the influence of a vortex field.
Electrical resistivity
It is also important to clarify what electrical conductivity is. Electrical conductivity is the reciprocal of resistance and is called electrical conductivity. This is an indicator showing the measure of conductivity of electric current.
Note! The larger it is, the better the conductor is able to conduct electricity.
General definition from the textbook