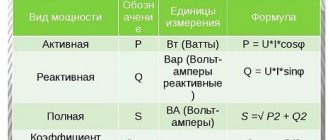
Magnetic induction is a vector quantity, which is a force characteristic of this magnetic field, namely a characteristic of its action on moving charged particles and on bodies with a magnetic moment.
Units of designation: SI unit is tesla (T), in GHS it is gauss (G) (relationship: 1 T = 104 G).
Magnetic induction formula:
B = Mmax / IS
Where: B – magnetic field induction (in T), Mmax – maximum torque of magnetic forces applied to the frame (in Nm), l – core length (in m), S – frame area (in m²)
Physical meaning of magnetic induction
Physically, this phenomenon is explained as follows. The metal has a crystalline structure (the coil is made of metal). The crystal lattice of a metal contains electrical charges - electrons. If no magnetic influence is exerted on the metal, then the charges (electrons) are at rest and do not move anywhere.
Dmitry Petrovich VasilievProfessor of Electrical Engineering, St. Petersburg State Polytechnic University If the metal comes under the influence of an alternating magnetic field (due to the movement of a permanent magnet inside the coil - namely movement), then the charges begin to move under the influence of this magnetic field.
As a result, an electric current arises in the metal. The strength of this current depends on the physical properties of the magnet and coil and the speed of movement of one relative to the other.
When a metal coil is placed in a magnetic field, the charged particles of the metal lattice (in the coil) are rotated at a certain angle and placed along the magnetic field lines.
The higher the strength of the magnetic field, the more particles rotate and the more uniform their arrangement will be.
Magnetic fields oriented in one direction do not neutralize each other, but add up, forming a single field.
Inductance
Electric current passing through a conductor creates a magnetic field around it. The magnetic flux \( \Phi \) through the loop of this conductor is proportional to the induction modulus \( \vec{B} \) of the magnetic field inside the loop, and the magnetic field induction, in turn, is proportional to the current strength in the conductor.
Therefore, the magnetic flux through the loop is directly proportional to the current in the loop:
Inductance is a coefficient of proportionality \( L \) between the current strength \( I \) in the circuit and the magnetic flux \( \Phi \) created by this current:
Inductance depends on the size and shape of the conductor, on the magnetic properties of the environment in which the conductor is located.
The SI unit of inductance is henry (H). The inductance of the circuit is 1 henry if, at a direct current of 1 ampere, the magnetic flux through the circuit is 1 weber:
We can give a second definition of the unit of inductance: an element of an electrical circuit has an inductance of 1 H if, with a uniform change in the current in the circuit by 1 ampere in 1 s, a self-inductive emf of 1 volt occurs in it.
Magnetic flux
Magnetic flux is a scalar quantity that characterizes the effect of magnetic induction on a certain metal circuit.
Magnetic induction is determined by the number of lines of force passing through 1 cm2 of the metal section.
The magnetometers used to measure it are called teslometers.
Abrahamyan Evgeniy PavlovichAssociate Professor, Department of Electrical Engineering, St. Petersburg State Polytechnic University The unit of measurement of magnetic induction in the SI system is Tesla (T).
After the movement of electrons in the coil ceases, the core, if it is made of soft iron, loses its magnetic qualities. If it is made of steel, then it has the ability to retain its magnetic properties for some time.
Magnet interaction
A permanent magnet (or magnetic needle) is oriented along the Earth's magnetic meridian. The end that points north is called the north pole (N), and the opposite end is called the south pole (S). Bringing two magnets closer to each other, we note that their like poles repel, and their opposite poles attract (Fig. 1).
If we separate the poles by cutting a permanent magnet into two parts, we will find that each of them will also have two poles, i.e., it will be a permanent magnet (Fig. 2). Both poles - north and south - are inseparable from each other and have equal rights.
The magnetic field created by the Earth or permanent magnets is represented, like an electric field, by magnetic lines of force. A picture of the magnetic field lines of a magnet can be obtained by placing a sheet of paper over it, on which iron filings are sprinkled in an even layer. When exposed to a magnetic field, the sawdust becomes magnetized - each of them has north and south poles. The opposite poles tend to move closer to each other, but this is prevented by the friction of the sawdust on the paper. If you tap the paper with your finger, the friction will decrease and the filings will be attracted to each other, forming chains depicting magnetic field lines.
In Fig. Figure 3 shows the location of sawdust and small magnetic arrows in the field of a direct magnet, indicating the direction of the magnetic field lines. This direction is taken to be the direction of the north pole of the magnetic needle.
MI vector direction
The direction of magnetic fields can be indicated by a magnet arrow placed in these fields. It will spin until it stops. The northern end of the arrow will show where B→ the unit vector of a particular field is oriented.
Magnetic induction lines
The frame with current behaves in the same way, having the ability to navigate the MP without interference. The direction of the induction vector indicates the orientation of the normal to such a closed electromagnetic circuit.
Attention! The rule of the gimlet (right screw) is used here. If the screw is rotated in the direction of the current in the frame, then the forward movement of the screw will coincide with the direction of the positive normal.
In some cases, the right-hand rule is used to find direction.
Visual display of MI lines
The line to which a tangent can be drawn, coinciding with B→, is called the magnetic induction (MI) line. Using such lines, you can visually display the magnetic field. These are closed contour lines that cover currents. Their density is always proportional to the value of B→ at a specific point in the MP.
Information. When dealing with the magnetic field of direct motion of charged particles, these lines are depicted as concentric circles. They have their center located in a straight line with the current, and are located in planes located at right angles to it.
The direction of magnetic lines can also be determined using the gimlet rule.
Ampere power
Ampere force is the force that acts on a current-carrying conductor in a magnetic field.
Ampere's law: a conductor with a current of force \( I \) of length \( l \), placed in a magnetic field with induction \( \vec{B} \), is acted upon by a force whose modulus is equal to:
where \( \alpha \) is the angle between the current-carrying conductor and the magnetic induction vector \( \vec{B} \).
The direction of the Ampere force is determined by the left hand rule : if the palm of the left hand is positioned so that the component of the magnetic induction vector \(B_\perp \) perpendicular to the conductor enters the palm, and four extended fingers indicate the direction of the current in the conductor, then the bent one The 90° thumb will show the direction of the Ampere force.
Ampere's force is not central. It is directed perpendicular to the lines of magnetic induction.
Ampere power is widely used. In technical devices, a magnetic field is created using conductors through which electric current flows. Electromagnets are used in an electromechanical relay for remotely turning off electrical circuits, a magnetic crane, a computer hard drive, a VCR recording head, a TV picture tube, and a computer monitor. Electric motors are widely used in everyday life, in transport and in industry. The interaction of an electromagnet with the field of a permanent magnet made it possible to create electrical measuring instruments (ammeter, voltmeter).
The simplest model of an electric motor is a current-carrying frame placed in the magnetic field of a permanent magnet. In real electric motors, instead of permanent magnets, electromagnets are used, and instead of a frame, windings with a large number of turns of wire are used.
Electric motor efficiency:
where \( N \) is the mechanical power developed by the engine.
The efficiency of the electric motor is very high.
Algorithm for solving problems about the action of a magnetic field on current-carrying conductors:
- make a schematic drawing on which to indicate a conductor or circuit with current and the direction of the field lines;
- mark the angles between the field direction and individual contour elements;
- using the left-hand rule, determine the direction of the Ampere force acting on a current-carrying conductor or on each element of the circuit, and show these forces in the drawing;
- indicate all other forces acting on the conductor or circuit;
- write down formulas for the remaining forces mentioned in the problem. Express forces in terms of the quantities on which they depend. If the conductor is in equilibrium, then it is necessary to write down the condition of its equilibrium (the sum of forces and moments of forces being equal to zero);
- write down Newton's second law in vector form and in projections;
- solve the resulting system of equations for an unknown quantity;
- check the solution.
Basic formulas for calculating the MI vector
The magnetic induction vector, the formula of which is B = Fm/I*∆L, can be found using other mathematical calculations.
Law of Electromagnetic Induction
The law of electromagnetic induction (Faraday's law) sounds like this:
The induced emf in a closed loop is equal and opposite in sign to the rate of change of the magnetic flux through the surface bounded by the loop.
Mathematically it can be described by the formula:
| Faraday's law Ɛi — induced emf [V] ΔФ/Δt — rate of change of magnetic flux [Wb/s] |
The “–” sign in the formula allows you to take into account the direction of the induction current. The induced current in a closed circuit is always directed so that the magnetic flux of the field created by this current through the surface bounded by the circuit would reduce those changes in the field that caused the appearance of the induced current.
If the circuit consists of N turns (that is, it is a coil), then the induced emf will be calculated as follows.
| Faraday's law for a circuit of N turns Ɛi — induced emf [V] ΔФ/Δt — rate of change of magnetic flux [Wb/s] N - number of turns [-] |
The strength of the induction current in a closed conductive circuit with resistance R:
| Ohm's law for a conductive circuit Ɛi — induced emf [V] I - induction current strength [A] R - circuit resistance [Ohm] |
If a conductor of length l moves with speed v in a constant uniform magnetic field with induction B the emf of electromagnetic induction is equal to:
| Induction emf for a moving conductor Ɛi — induced emf [V] B—magnetic induction [T] v—conductor speed [m/s] l - conductor length [m] |
The occurrence of induced emf in a conductor moving in a magnetic field is explained by the action of the Lorentz force on free charges in moving conductors. The Lorentz force plays the role of an external force in this case.
A conductor moving in a magnetic field through which an induced current flows experiences magnetic braking. The total work done by the Lorentz force is zero.
The amount of heat in the circuit is released either due to the work of an external force, which maintains the speed of the conductor unchanged, or due to a decrease in the kinetic energy of the conductor.
A change in the magnetic flux penetrating a closed circuit can occur for two reasons:
- due to movement of the circuit or its parts in a time-constant magnetic field. This is the case when conductors, and with them free charge carriers, move in a magnetic field
- due to changes in time of the magnetic field with a stationary circuit. In this case, the occurrence of induced emf can no longer be explained by the action of the Lorentz force. The phenomenon of electromagnetic induction in stationary conductors, which occurs when the surrounding magnetic field changes, is also described by Faraday's formula
Thus, the phenomena of induction in moving and stationary conductors proceed in the same way, but the physical reason for the occurrence of induction current turns out to be different in these two cases:
- in the case of moving conductors, the induced emf is due to the Lorentz force
- in the case of stationary conductors, the induced emf is a consequence of the action on free charges of the vortex electric field that occurs when the magnetic field changes.
Biot-Savart-Laplace Law
Induction EMF formula
Describes the rules for finding B→ magnetic field, which creates a constant electric current. This is an experimentally established pattern. Biot and Savard identified it in practice in 1820, Laplace managed to formulate it. This law is fundamental in magnetostatics. During the practical experiment, a stationary wire with a small cross-section was considered, through which an electric current was passed. For study, a small section of wire was selected, which was characterized by the vector dl. Its module corresponded to the length of the section under consideration, and its direction coincided with the direction of the current.
Interesting. Laplace Pierre Simon proposed to consider even the movement of one electron as a current and, based on this statement, using this law, he proved the possibility of determining the magnetic field of an advancing point charge.
According to this physical rule, each segment dl of a conductor through which electric current I flows forms a magnetic field dB in the space around itself at an interval r and at an angle α:
dB = µ0 *I*dl*sin α /4*π*r2,
Where:
- dB – magnetic induction, T;
- µ0 = 4 π*10-7 – magnetic constant, H/m;
- I – current strength, A;
- dl – conductor section, m;
- r – distance to the point where the magnetic induction is located, m;
- α is the angle formed by r and the vector dl.
Important! According to the Biot-Savart-Laplace law, by summing the magnetic field vectors of individual sectors, it is possible to determine the MF of the desired current. It will be equal to the vector sum.
Biot-Savart-Laplace Law
There are formulas that describe this law for individual cases of MP:
- fields of direct movement of electrons;
- fields of circular motion of charged particles.
The formula for MP of the first type is:
B = µ* µ0*2*I/4*π*r.
For circular motion it looks like this:
B = µ*µ0*I/4*π*r.
In these formulas, µ is the magnetic permeability of the medium (relative).
The law under consideration follows from Maxwell's equations. Maxwell derived two equations for the magnetic field; the case where the electric field is constant is considered by Biot and Savart.
Superposition principle
For MF, there is a principle according to which the total vector of magnetic induction at a certain point is equal to the vector sum of all MI vectors created by different currents at a given point:
B→= B1→+ B2→+ B3→… + Bn→
Lenz's rule
To determine the direction of the induced current, you need to use Lenz's rule.
Academically, this rule is as follows: the induced current excited in a closed loop when the magnetic flux changes is always directed in such a way that the magnetic field it creates prevents the change in the magnetic flux causing the induced current.
Let's try a little simpler: the coil in this case is a dissatisfied granny. They take away her magnetic flux - she is unhappy and creates a magnetic field, which this magnetic flux wants to take back.
They give her a magnetic flux, take it, they say, use it, and she’s like, “Why did I give up your magnetic flux!” and creates a magnetic field, which expels this magnetic flux.
Lorentz force
The Lorentz force is a force acting on a moving charged particle from a magnetic field.
Formula for finding the Lorentz force:
where \( q \) is the particle charge, \( v \) is the particle velocity, \( B \) is the magnitude of the magnetic induction vector, \( \alpha \) is the angle between the particle velocity vector and the vector of magnetic induction.
The direction of the Lorentz force is determined by the left hand rule : if the palm of the left hand is positioned so that the component of the magnetic induction vector \( B_\perp \) perpendicular to the conductor enters the palm, and four extended fingers indicate the direction of the velocity of the positively charged particle, then the bent at 90° the thumb will show the direction of the Lorentz force.
If the charge of the particle is negative, then the direction of the force is reversed.
Important! If the velocity vector is co-directed with the magnetic induction vector, then the particle moves uniformly and rectilinearly.
In a uniform magnetic field, the Lorentz force bends the trajectory of a particle.
If the velocity vector is perpendicular to the magnetic induction vector, then the particle moves in a circle whose radius is equal to:
where \( m \) is the mass of the particle, \( v \) is the velocity of the particle, \( B \) is the magnitude of the magnetic induction vector, \( q \) is the charge of the particle.
In this case, the Lorentz force plays the role of a centripetal force and its work is zero. The period (frequency) of revolution of a particle does not depend on the radius of the circle and the speed of the particle. Formula for calculating the period of revolution of a particle:
Angular velocity of a charged particle:
Important! The Lorentz force does not change the kinetic energy of the particle and its velocity modulus. Under the influence of the Lorentz force, the direction of the particle's velocity changes.
If the velocity vector is directed at an angle \( \alpha \) (0° < \( \alpha \) < 90°) to the magnetic induction vector, then the particle moves along a helical line.
In this case, the particle velocity vector can be represented as the sum of two velocity vectors, one of which, \( \vec{v}_2 \), is parallel to the vector \( \vec{B} \), and the other, \( \vec {v}_1\), – is perpendicular to it. The vector \( \vec{v}_1 \) does not change either in magnitude or direction. The vector \( \vec{v}_2 \) changes in direction. The Lorentz force will impart an acceleration to the moving particle perpendicular to the velocity vector \( \vec{v}_1 \). The particle will move in a circle. The period of revolution of a particle in a circle is \( T \).
Thus, uniform motion along the induction line will be superimposed on circular motion in a plane perpendicular to the vector \( \vec{B} \). The particle moves along a helical line with a step \( h=v_2T \).
Important! If a particle moves in electric and magnetic fields, then the total Lorentz force is equal to:
The peculiarities of the movement of a charged particle in a magnetic field are used in mass spectrometers - devices for measuring the masses of charged particles; particle accelerators; for thermal insulation of plasma in Tokamak installations.
Algorithm for solving problems about the action of a magnetic (and electric) field on charged particles:
- make a drawing, indicate the magnetic (and electric) field lines on it, draw the vector of the initial velocity of the particle and note the sign of its charge;
- depict the forces acting on a charged particle;
- determine the type of particle trajectory;
- expand the forces acting on a charged particle along the direction of the magnetic field and in the direction perpendicular to it;
- draw up the basic equation for the dynamics of a material point for each of the directions of force distribution;
- express forces through the quantities on which they depend;
- solve the resulting system of equations for an unknown quantity;
- check the solution.