In this article we will consider a universal method for calculating beam deflections - the method of initial parameters . Like any other article for dummies, this material will be presented as simply, concisely and without unnecessary abstruse terms.
As an example, let's take a metal beam on two supports. Let us write down a formula for calculating the deflection and calculate its numerical value. And also at the end of this article I will provide links to other useful articles with examples of determining deflections for various design schemes.
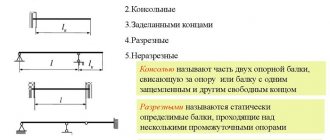
What is beam deflection?
Under the action of an external load, the cross sections of the beam move vertically (up or down), these movements are called deflections . In addition, the sections are rotated at a certain angle. These two quantities, for any section, can be determined using the initial parameters method.
ν-deflection of section C; θ is the rotation angle of section C.
Calculation of deflections is necessary to perform stiffness calculations. A beam can be considered rigid only if the calculated deflections do not exceed the permissible values. If the rigidity condition is not met, then measures are taken to increase it. For example, they are set by another material, which has a GREATER elastic modulus. Or they change the geometric parameters of the beam, most often the cross section. For example, if an I-profile beam No. 12 is not suitable in terms of rigidity, I-beam No. 14 is accepted and a recalculation is made. If necessary, repeat the selection until they find the right one - the I-beam.
Review[edit]
Typical section of I-beams.
There are two standard forms of I-beam:
- I-beam products produced by hot rolling, cold rolling or extrusion (depending on the material).
- A plate beam, formed by welding (or sometimes bolting or riveting) plates.
I-beams are typically made from structural steel, but can also be made from aluminum or other materials. A common type of I beam is the rolled steel beam
(RSJ), sometimes incorrectly displayed as a
reinforced steel beam
. British and European standards also specify universal beams (UB) and universal columns (UC). These sections have parallel flanges, unlike the various thickness RSJ flanges which are now rarely rolled in the UK. Parallel flanges are easier to connect and eliminate the need for tapered washers. UCs have equal or nearly equal width and depth and are more suitable in a vertical orientation to carry an axial load, such as columns in a multi-story structure, while UBs are significantly deeper than their width and are more suitable to carry a bending load, such as a beam elements in the floors.
I-beams—I-beams made from wood with fiberboard and/or laminated timber—are also becoming increasingly popular in construction, especially in residential buildings, because they are lighter and less prone to warping than solid wood beams. However, there was some concern about their rapid loss of strength in fire if they were not protected.
Initial parameters method
The initial parameters method is a fairly universal and simple method. Using this method, you can write a formula to calculate the deflection and rotation angle of any section of a beam of constant stiffness (with the same cross-section along the length).
The initial parameters are understood as already known movements:
- deflections in supports are zero;
- in a rigid embedment, the deflection and rotation angle of the section are zero.
Taking into account these properties, they are also called boundary conditions, displacements in other parts of the beam are determined.
Hypotheses and definitions for bending
First of all, let's start with the definitions and hypotheses that we introduce in the strength of materials when studying bending:
What is a beam? A beam is a rod whose length is significantly greater than its width and height. At the same time, it experiences bending deformation.
beam - called a structural element when the length is significantly greater than the width and height
Bend , what is it? This is a type of deformation in which the longitudinal axis of the beam is bent, but the longitudinal fibers do not press on each other, and the sections are flat before bending and remain so after bending.
bending sign rule
The figure above shows a diagram for deriving the stress formula and a demonstration of the stresses that arise during pure bending. This term will have to be explained in another article. In the meantime, let's continue.
A diagram is a graph of changes in the quantity for which it is constructed. So the bending moment diagram is a graph of the change in internal force - bending moment along the length of the beam. Using this graph, plotted to scale, you can use simple operations to determine the value of the bending moment at any point along the length of the beam. Diagram of shear force - similarly, a graph of its change in internal force - shear force along the length of the beam.
Calculation of beam deflections
Let's see how to use the initial parameters method using the example of a simple beam, which is loaded with all kinds of loads, in order to maximally cover all the subtleties of this method:
Support reactions
To make the calculation, you need to know all the external loads acting on the beam, including the reactions occurring in the supports.
If you don’t know how to determine reactions, then I recommend studying this material, where I tell you how they are determined using the example of the same beam:
Coordinate system
Next, we introduce a coordinate system with the origin on the left side of the beam (point A):
Distributed load
The initial parameters method, which we will use a little later, only works when the distributed load reaches the rightmost section, the one farthest from the origin of the coordinate system. Specifically, in our case, the load breaks and such a design scheme is unacceptable for further calculations.
If the load were applied like this:
Then we could immediately begin calculating displacements. We will need to use one tricky trick - introduce additional loads, one of which will continue the existing load q, the other will compensate for this artificial continuation. Thus, we obtain an equivalent design scheme, which can already be used in the calculation using the initial parameters method:
Here, in fact, are all the preparatory steps that need to be done before the calculation.
Let's proceed directly to the calculation of the beam deflection itself. Let's consider the section in the middle of the span - section C:
We write down the boundary conditions relative to the coordinate system. Taking into account the method of securing the beam, we fix that the deflections at points A and B are equal to zero, and the distances from the origin to the supports are important:
\[ { V }_{ A }=0\quad at\quad x=0 \]
\[ { V }_{ B }=0\quad at\quad x=8m \]
We write the equation of the initial parameters method for section C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
The product of the beam stiffness EI and the section deflection C will be the sum of the product EI and the section deflection at the origin of the coordinate system, that is, section A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Let me remind you that E is the modulus of elasticity of the first kind, depending on the material from which the beam is made, I is the moment of inertia, which depends on the shape and dimensions of the cross section of the beam. The angle of rotation of the cross section at the origin of the coordinate system is also taken into account, and the angle of rotation is additionally multiplied by the distance from the section in question to the origin of coordinates:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A } \cdot 4+… \]
Accounting for external load
And finally, you need to take into account the external load, but only that which is located to the left of the section C under consideration. There are several features here:
- Concentrated forces and distributed loads that are directed upward, that is, coincide with the direction of the y-axis, are written in the equation with a plus sign. If they are directed downward, respectively, with a minus sign:
- Moments directed clockwise are positive, counterclockwise are negative:
- All concentrated moments need to be multiplied by the fraction:
\[ M\cdot \frac { { x }^{ 2 } }{ 2 } \]
- All concentrated forces need to be multiplied by the fraction:
\[ F\cdot \frac { { x }^{ 3 } }{ 6 } \]
- The beginning and end of distributed loads must be multiplied by a fraction:
\[ q\cdot \frac { { x }^{ 4 } }{ 24 } \]
Where did these numbers and degrees come from? All these things follow when integrating the differential equation of the elastic line of a beam; in the method of initial parameters, all these conclusions are omitted, that is, it is, as it were, a simplified and universal method.
Deflection formulas
Taking into account all the rules described above, we write the final equation for section C:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A } \cdot 4+\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q \cdot { 2 }^{ 4 } }{ 24 } \]
This equation contains 2 unknown quantities - the desired deflection of the section C and the angle of rotation of the section A.
Therefore, in order to find the deflection, we will compose a second equation for section B, from which we can determine the angle of rotation of section A. At the same time, we will fix the material passed through:
\[ E{ I }_{ z }{ V }_{ B }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A } \cdot 8+\frac { { R }_{ A }\cdot { 8 }^{ 3 } }{ 6 } -\frac { F\cdot { 8 }^{ 3 } }{ 6 } -\frac { q \cdot 6^{ 4 } }{ 24 } +\frac { q\cdot 2^{ 4 } }{ 24 } =0 \]
Let's simplify the equation:
\[ E{ I }_{ z }{ \theta }_{ A }\cdot 8+874.67=0 \]
Expressing the angle of rotation:
\[ { \theta }_{ A }=-\frac { 874.67 }{ 8E{ I }_{ z } } =-\frac { 109.33 kN{ m }^{ 2 } }{ E{ I }_{ z } } \]
We substitute this value into our first equation and find the desired displacement:
\[ E{ I }_{ z }{ V }_{ C }=\frac { -109.33\cdot 4E{ I }_{ z } }{ E{ I }_{ z } } +\frac { { R }_{ A }\cdot { 4 }^{ 3 } }{ 6 } -\frac { F\cdot { 4 }^{ 3 } }{ 6 } -\frac { q\cdot { 2 }^{ 4 } }{ 24 } =-\frac { 280kN{ m }^{ 3 } }{ E{ I }_{ z } } \]
Constructing diagrams of bending moment and shear force during bending
The obtained values of the bending moment and shear force in two sections (at positions x=0 and x=l) are plotted according to the corresponding ordinates, i.e. we literally build graphs of both functions.
constructing diagrams for bending internal moment forces M(x) and Q(x)
What do we see from the constructed diagrams, what conclusions can we draw:
- from the diagram of the transverse force it is clear that it does not change along the entire length and is equal to the external force F
- since at the origin of coordinates x (i.e. on the right) we see on the diagram a “jump” by the magnitude of this force, then at the end, in the embedment, the jump indicates that the reaction in the embedment is equal to the force F
- on the moment diagram, the graph leaves zero coordinate x (on the right on the beam) and the moment is also zero
- As the section moves away from the force to the left, the moment increases and reaches its greatest value in the embedment, where the same jump is observed as in the transverse force diagram and is equal to (- F x). This indicates that the moment in the seal is equal to exactly this value
What is a “jump” on a diagram?
When the graph does not start from zero or not from the value obtained in the previous section, but has two different values in the same section x, such a discontinuity in the function is called a jump. Those. if we look at the graph infinitely close on the left and infinitely close on the right, we get two different values for both shear force and moment. And this jump for the transverse force must be equal to the applied concentrated force, and for the moment, the applied concentrated moment.
That's all the secrets of constructing diagrams for moments and shear forces. Of course, the process itself becomes a little more complicated, but the principle remains the same.
Further in the video, examples of constructing diagrams for a distributed bending moment load are presented. To make it easier to show the difference, everything is collected in one video:
Links[edit]
- Thomas Derdak, Jay P. Pederson (1999). International Directory of Company Histories. 26
. St. James Press. p. 82. ISBN 978-1-55862-385-9. - ↑
Morning Call (2003).
"Forging America: The Story of Bethlehem Steel". Addition to the morning call
.
Allentown, Pennsylvania, USA: Morning call. A detailed history of the company from journalists from Morning Call staff. - ^ ab Geer and Timoshenko, 1997, Mechanics of Materials
, PWS Publishing. - “ASTM A992 Standard Specification? A992M for structural steel profiles". American Society for Testing and Materials. 2006. DOI: 10.1520/A0992_A0992M-06A.
- ^ ab Hot Rolled Steel and Structural Steel Products - Fifth Edition. Archived April 10, 2013 at the Wayback Machine - Onesteel. Retrieved December 18, 2015.
- AISC Manual of Steel Structures, 14th Edition
- Handbook of Steel Construction
(9th ed.). Canadian Institute of Steel Construction. 2006. ISBN 978-0-88811-124-1. - IMCA Manual of Steel Structures, 5th Edition.
- "Structural Sections" (PDF). Corus Construction & Industrial. Archived from the original (PDF) on February 15, 2010.
- "Cellular Beams - Kloeckner Metals UK". kloecknermetalsuk.com
. Retrieved May 13, 2022.