How are operating strength indicators calculated?
The strength of cables and ropes for production purposes is regulated by the relevant GOSTs:
- GOST 2688-80 – steel ropes, cables, slings for cranes (construction, metallurgical), installations in mines;
- GOST 3068-88 – ropes and cables for road, construction equipment, lifting and transport mechanisms, earth-moving equipment;
- GOST 7668-80 – universal steel cables for metallurgical, industrial lifting works, construction;
- GOST 7669-80 – cables and ropes for winches, excavator buckets, mine hoists;
The strength of a steel cable is determined by two criteria:
- tensile strength of cables is a calculated value that determines at what minimum loads the steel cable begins to fail;
- working strength or permissible force is an indicator of operational capabilities, optimal loads on the cable under which it can be operated for a certain period without breaks or destruction. This indicator determines what working loads are permissible for a steel rope.
Tensile and working strength depends on production technology, design, and degree of rigidity. The higher the rigidity of the cable, the higher the tensile strength.
How long does a 12mm cable last?
Characteristics of steel cables
| Cable diameter , mm | Estimated weight of 100 linear meters of cable , kg | Estimated tensile strength of cable , kg/ mm 2 |
| 12.0 | 59,27 | 9090 |
| 13,5 | 74,95 | 11450 |
| 15,0 | 92.50 | 14150 |
| 16,5 | 111.9 | 17 150 |
Application area
The use of steel rope can be found in various fields. This can be as a cable for mounting a tent and cable-stayed roof structures to suspension bridges and television and radio towers.
Different applications for wire ropes place different demands on strength, abrasion and corrosion resistance. To meet these requirements, the cable is made of materials such as:
- Stainless steel. Used where corrosion is a major factor.
- Galvanized carbon steel. It is used where strength comes first and corrosion resistance is less important.
The wire (one element) can have a cross-section of up to 3 mm. This is enough to withstand loads of up to 200 kgf/mm2. Steel cables and ropes differ in terms of lay, which can be single, double or triple. The arrangement of the wire in different layers has one of the following tangents:
- point (usually used for minor intermittent loads);
- linear (used in many areas);
- point-linear (used for additional strength).
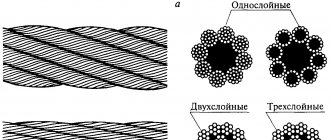
Classification of steel ropes
Depending on the type of laying of the strands, the following types of steel ropes are distinguished:
- The wires between the layers have a point contact - TK;
- Between the layers of wire there is a linear contact - LC;
- Linear contact and the same diameter of wires in each layer of the strand - LK-O;
- Linear contact and the presence of wires of different diameters in the outer layer - LK-R;
- Linear contact between filling wires and individual layers - LK-Z;
- Linear contact and the presence of strands with both wires of the same and different diameters - LK-RO;
- Combined point-linear contact of wires - TLC.
To work on drums and blocks with semicircular grooves, it is better to choose steel ropes with a linear touch. This is due to the fact that their service life is almost twice as long as that of TKL brand ropes.
Depending on the core material used, there are:
- Ropes with an organic core made from synthetic or natural materials – O.S. This type of core, thanks to its special impregnation, prevents rapid abrasion of the wires and protects the internal parts of the rope from corrosive processes;
- Ropes with a metal core – M.S. This type of steel rope is excellent for use in hot shops, as well as in cases where multi-layer winding on a drum is used.
According to the laying method, the following types of ropes are distinguished:
- Non-unwinding - N. In them, the strands retain their properties after the welding and dressing are removed from the end of the rope;
- Unwinding - R. In ropes of this type, after removing the welding or tying, the wires and strands change their position.
When making non-unwinding ropes, the wires are subjected to preliminary bending. Thanks to this, this type has greater durability, less tendency to form loops and knots, as well as torsion.
Depending on the direction of lay, steel ropes of left (L) and right (R) lay are distinguished.
There are various options for laying elements and the rope itself in triple and double lay products. In accordance with this, steel ropes are distinguished:
- One-way lay - O. They have the same direction of lay of the strands and lay of the rope itself along the outer wire.
- Cross lay. They are characterized by the opposite direction of laying of strands and strands and laying of the rope. For triple lay ropes, only this type of lay is used.
- Combined lay - K. The direction of lay of the strands alternates through one strand.
Products with cross lay are recommended for working ropes on blocks with wedge-shaped grooves or with an undercut, flat rims, as well as for cranes. In cases where the possibility of rope torsion is excluded, it is better to use ropes with one-sided lay.
Steel ropes also differ in degree of twist:
- MK - low-rotating. They are characterized by the presence of opposite direction of laying of individual elements in layers.
- Twisting - have the same direction of all strands in the strand.
Depending on the physical and mechanical characteristics of the wire, the following types of steel ropes are distinguished:
- Brand B. These ropes are used exclusively in particularly complex and critical cases.
- Grade I. Most often used as crane rope.
- Mark II.
Also, depending on the characteristics of the wire surface coating, steel ropes are classified into the following types:
- Without any coating;
- With zinc coating - coolant. Used to work in conditions with a particularly aggressive external environment;
- With zinc coating and designed for work in aggressive environments – F;
- With zinc coating for operation in medium aggressive environmental conditions – C;
- With coating of strands or the rope itself with artificial materials - P.
Steel ropes intended for cargo purposes are marked GL, and for cargo purposes - G.
According to manufacturing accuracy, ropes with increased T and normal H accuracy are distinguished.
Example of rope symbols
Surface Density of Zinc Steel Rope
| Nominal diameter, mm | Surface density of zinc, g/m2, not less, for wire groups | ||
| WITH | AND | coolant | |
| 0.20 to 0.24 | 15 | 20 | 30 |
| >0.24 to 0.32 | 20 | 25 | 45 |
| >0.32 to 0.38 | 20 | 25 | 60 |
| >0.38 to 0.45 | 30 | 40 | 75 |
| >0.45 to 0.55 | 35 | 40 | 90 |
| >0.55 to 0.65 | 40 | 50 | 110 |
| >0.65 to 0.75 | 40 | 60 | 120 |
| >0.75 to 0.95 | 50 | 70 | 130 |
| >0.95 to 1.15 | 60 | 80 | 150 |
| >1.15 to 1.40 | 60 | 90 | 165 |
| >1.40 to 1.80 | 70 | 100 | 180 |
| >1.80 to 2.40 | 80 | 110 | 205 |
| >2.40 to 3.00 | 90 | 125 | 230 |
| >3.00 to 3.80 | 100 | 135 | 230 |
| >3.80 to 4.40 | 110 | 150 | 245 |
| >4.40 to 5.10 | 110 | 165 | 245 |
Direction and combination of lay directions of steel rope:
When installing ropes, the main requirement is to prevent them from unwinding. To do this you need the following:
- The drum with the rope should be placed on the unwinding device so that its axis is strictly horizontal.
- The winding end should be located at the top or bottom of the drum.
- The drum should slow down slightly during the winding process.
- The distance between two drums must be greater than three hundred diameters of the steel rope.
During installation, rope kinks, especially alternating ones, should be avoided.
How to measure rope diameter
“Nominal Diameter” defines the design diameter of the rope. In order to measure the actual diameter, you must use a caliper, the length of the jaws of which must be more than ¾ of the diameter of the rope being measured.
Measurements should be taken in two cross sections located at a distance of at least one meter from each other. At each of these points, measurements are taken in two planes perpendicular to each other. After receiving all four results, their arithmetic mean is calculated. For a new rope, the resulting figure should be located within the tolerance field of the “nominal” diameter.
Unwinding rope from a coil
The coil should be placed on the ground and the rope should begin to unwind strictly in a straight line, while trying to prevent contamination of its surface with moisture, metal chips, soil or any other harmful substances.
The coil can also be installed on a rotary unwinder. After this, the coil is rotated by pulling the outer end of the rope.
It is impossible to unwind ropes from fixed coils, as this leads to the formation of loops and twisting of the ropes, and this in turn significantly reduces their performance.
Picture 1.
Never unwind a rope from a fixed coil, as this may cause the rope to twist and form loops, which will significantly reduce the performance of the rope (Fig. 2).
Figure 2.
Wrong.
Note the formation of loops.
Elastic forces: springs, ropes and threads
The problems in this article consider cases when a body is raised or lowered with acceleration. At the same time, the tension of the thread on which the load is suspended is different. Examples are given of composing equations according to Newton's second law in projections on the axis.
Problem 1. A truck towed a passenger car weighing m and, moving uniformly accelerated, traveled m in s. How much does the cable connecting the cars lengthen if its stiffness is N/m? Ignore friction.
The elongation of the cable can be found by knowing the elastic force:
Since friction does not need to be taken into account, then according to Newton’s second law
Hence,
Let's determine the acceleration of the truck:
Finally, to lengthen the cable we get:
The answer was obtained in meters; you can write it in mm: 0.64 mm.
Problem 2. On a thread supporting tension H, a load of mass kg is lifted from rest vertically upward. Assuming the motion to be uniformly accelerated, find the maximum height to which the load can be raised in c so that the thread does not break.
To task 2
Let's write Newton's second law in projection onto the vertical axis:
Then the acceleration is:
The height to which a body can be raised with such acceleration is equal to
Answer: 5 m
Problem 3. A rope supports a load weighing kg when lifting it vertically with some acceleration, and a load weighing kg when lowering it with the same acceleration. What is the maximum weight that can be raised or lowered on this rope at a constant speed?
To problem 3
Let us write the equations according to the second law for both the ascent and descent of the body. Let's direct the axis upward, then when lifting:
When descending:
Acceleration according to the condition is the same, then:
Or
By equating, we can find the tension force of the rope that it can withstand:
If a load of mass were simply hanging on such a rope, then we would write
Hence,
Answer: 190 kg
Problem 4. A load with a mass of kg is suspended from a spring with a stiffness of N/m. The length of the spring in the unstretched state is m. Find the length of the spring when the load hangs on it. What will be the length of the spring if the spring with a load is in an elevator moving with acceleration m/s directed a) upward; b) down?
To problem 4
If a load is hung on a spring, its length increases:
When the elevator moves upward, we write down the second law (the axis is directed upward):
Then the length of the spring in this case:
When the elevator moves downward, we write the second law (the axis is directed upward):
Then the length of the spring in this case:
Answer: , , .
Problem 5. The load is secured to the cart by four stretched threads. The tension forces of the horizontal threads are and , respectively, and the vertical threads are and . With what acceleration does the cart move on a horizontal plane?
To problem 5
Let's write the equations according to the second law in projections on the axes, which we will arrange traditionally: the axis is to the right, the axis is up. Then, if the cart moves to the right, along the axis, we have:
From the second equation we find the mass of the load:
Then the acceleration of the cart (and the load) is equal to:
If the cart moves to the left (against the axis), then only the first equation will change:
Then the acceleration of the cart (and the load) is equal to: