Ratio of shear stress to shear strain
| Shear modulus | |
| Common symbols | G, S |
| SI unit | pascal |
| Derivatives from other quantities | G = / G = / 2 (1+ ) |
Shear strain
In materials science, shear modulus
or
modulus of stiffness
, denoted
G
, or sometimes
S
or
M
, is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to shear strain: [1]
g = d e f τ x y γ x y = F / A Δ X / l = F l A Δ X {\displaystyle G\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\tau _{xy}}{\gamma _{xy}}} ={\frac {F/A}{\Delta x/l}}={\frac {Fl}{A\Delta x}}}
where
τ xy = F / A {\displaystyle \tau _{xy}=F/A\,} = shear stress F {\displaystyle F} is the force that acts A {\displaystyle A} is the area that the force γ acts on xy {\displaystyle \gamma _{xy}} = shear strain. In mechanical engineering, in other := Δ x / l = tan θ {\displaystyle :=\Delta x/l=\tan \theta } := θ {\displaystyle :=\theta } Δ x {\displaystyle \Delta x } lateral displacement l {\displaystyle l} initial length
The derived unit of shear modulus in the system is the pascal (Pa), although it is usually expressed in gigapascals (GPa) or thousand pounds per square inch (ksi). Its dimensional form is M 1 l -1 T -2, replacing the forces
for
mass
acceleration
times .
Explanation[edit]
| Material | Typical values for shear modulus (GPa) (at room temperature) |
| Diamond [2] | 478,0 |
| Steel [3] | 79,3 |
| Iron [4] | 52,5 |
| Copper [5] | 44,7 |
| Titan [3] | 41,4 |
| Glass [3] | 26,2 |
| Aluminum [3] | 25,5 |
| Polyethylene [3] | 0,117 |
| Rubber [6] | 0,0006 |
| Granite [7] [8] | 24 |
| Slate [7] [8] | 1.6 |
| Limestone [7] [8] | 24 |
| Chalk [7] [8] | 3,2 |
| Sandstone [7] [8] | 0,4 |
| Tree | 4 |
Shear modulus is one of several quantities for measuring the stiffness of materials. They all arise in the generalized Hooke's law:
- Young's modulus E
describes the deformation response of a material to a uniaxial stress in the direction of that stress (for example, pulling on the ends of a wire or placing a weight on the top of a column, causing the wire to become longer and the column to lose height). - the Poisson's ratio ν
describes the response in directions orthogonal to this uniaxial stress (the wire becomes thinner and the column thicker), - the bulk modulus of elasticity K
describes the response of a material to (uniform) hydrostatic pressure (e.g. pressure at the bottom of an ocean or deep pool), - The shear modulus G
describes the response of a material to shear stress (like cutting it with blunt scissors). These modules are not independent, and for isotropic materials they are related by the equations. [9] 2 G ( 1 + ν ) = E = 3 K ( 1 − 2 ν ) {\displaystyle 2G(1+\nu )=E=3K(1-2\nu )}
Shear modulus relates to the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite side experiences an opposing force (such as friction). If an object is shaped like a rectangular prism, it deforms into a parallelepiped. Anisotropic materials such as wood, paper, and virtually all single crystals exhibit different material responses to stress or strain when tested in different directions. In this case, it may be necessary to use the full tensor expression of the elastic constants rather than a single scalar value.
One possible definition of a fluid is a material with zero shear modulus.
Effect of temperature and pressure
As you would expect, the response of a material to an applied force varies with temperature and pressure. In metals, the shear modulus generally decreases with increasing temperature. Hardness decreases with increasing pressure. Three models are used to predict the effect of temperature and pressure on the shear modulus: the mechanical threshold stress (MTS) plastic flow model, the Nadal and Lepoak shear modulus (NP) model, and the Steinberg-Cochran-Guinan (SCG) shear modulus. model. For metals, there is usually a region of temperature and pressure in which the change in shear modulus is linear. Beyond this range, the modeling behavior is more complex.
Marking
Spring-spring steels can be grouped by position:
- unalloyed with a carbon content of 65-85% - inexpensive general purpose steel;
- manganese-silicon - the cheapest with high physical and chemical properties;
- chrome-manganese - stainless steel, works in aggressive environments at t -250 +250 C;
- additionally alloyed and/or tungsten, vanadium, boron - they are steels with an increased service life due to their homogeneous structure, an excellent strength-to-ductility ratio due to fine grains and can withstand high mechanical loads. They are used on such objects as railway transport.
Marking of spring steels is carried out as follows. Let's look at the example of 60S2HFA:
- 60 - percentage of carbon in tenths (carbon is not indicated in a letter value);
- C2 - letter designation of silicon with index 2, indicates a 2-fold increase in the standard content (1-1.5%);
- X - presence of chromium up to 0.9-1%;
- F - tungsten content up to 1%;
- A - the added letter index A at the end of the marking indicates the minimum content of harmful impurities of phosphorus and sulfur, no more than 0.015%.
Tensile strength
Solids are capable of withstanding limited loads; exceeding the limit leads to destruction of the metal structure, the formation of noticeable chips or microcracks. The occurrence of defects is associated with a decrease in performance properties or complete destruction. The strength of alloys and finished products is checked on test benches. The standards provide for a number of tests:
- Prolonged use of deforming force;
- Short-term and long-term shock impacts;
- Tension and compression;
- Hydraulic pressure, etc.
In complex mechanisms and systems, the failure of one element automatically causes increased loads on others. As a rule, destruction begins in those areas where stress is maximum. The safety margin serves as a guarantee of equipment safety in emergency situations and extends its service life.
Source of the article: https://e-metall.ru/blog/uprugost-stali/
Modulus of elasticity of steel
Editorial team E-metall Published 2021-03-27
When designing steel products or structural elements, the ability of the alloy to withstand multidirectional types of loads is taken into account: impact, bending, tensile, compressive. The value of the elastic modulus of steel, along with hardness and other characteristics, shows resistance to these influences.
For example, in reinforced concrete construction, longitudinal and transverse reinforcing bars are used. In the horizontal plane they are subject to tension, and in the vertical plane they are subject to pressure from the entire mass of the structure. In places where stress is concentrated: corners, technological openings, elevator shafts and flights of stairs, more reinforcement is placed. The ability of concrete to absorb water causes constant changes in compressive and tensile loads.
Let's look at another example. During wartime, many developments in the field of aviation were created. The most common causes of accidents were engine fires. Taking off from the ground, the plane enters atmospheric layers with rarefied air and its body expands; the reverse process occurs during landing. In addition, the structure is affected by the resistance of air flows, the pressure of curved layers of air and other forces. Despite their strength, the alloys existing at that time were not always suitable for the manufacture of critical parts; this mainly led to ruptures of fuel tanks.
In various types of industry, parts of moving mechanisms are made from steel: springs, leaf springs. The grades used for such purposes are not prone to cracking under constantly changing loads.
Methods for determining and monitoring strength indicators of metals
The development of metallurgy and other related areas for the production of metal objects is due to the creation of weapons. At first they learned to smelt non-ferrous metals, but the strength of the products was relatively low. Only with the advent of iron and its alloys did the study of their properties begin.
The first swords were made quite heavy to give them hardness and strength. Warriors had to take them in both hands to control them. Over time, new alloys appeared and production technologies were developed. Light sabers and swords came to replace heavy weapons. At the same time, tools were created. With increasing strength characteristics, tools and production methods were improved.
- Types of loads
- The concept of elastic modulus
- Table 1: Modulus of elasticity for metals and alloys
- Elastic modulus for different steel grades
- Table 2: Elasticity of steels
- Strength modules
- Table 3: Strength moduli for steels
Calculation of a compression spring made of rectangular wire.
The stiffness of a spring made of wire or a rectangular rod with the same dimensions as one made of round wire can be much greater. Accordingly, the compression force of the spring may be greater.
The program presented below is a revised version of the program for calculating cylindrical springs made of round wire , a detailed description of which you will find by following the link. Read this article and it will be easier for you to understand the algorithm.
may have guessed, is the determination of the coil stiffness ( C1 ) , which determines the spring stiffness ( C ) as a whole.
The following is a screenshot of the program and formulas for a cylindrical steel spring made of rectangular wire, in which ¾ of the turns are pressed at each end and the supporting surfaces are ground to ¾ of the circumference.
Attention!!!
After performing the calculation according to the program, check the tangential stresses!!!
4. I =( D1 / B) -1
5. At 1/3 : Y =5.3942*( H / B )2-0.3572*(H/B)+0.5272
At 1 : Y =5.4962*( H / B )(-1.715)
At 2< H / B <6 : Y = 3.9286 *( H / B )(- 1.2339 )
6. For H < B : C1 =(78500* H 4 )/( Y* ( D1 - B )3)
When H > B : C1 =(78500* B 4 )/( Y* ( D1 - B )3)
8. Tnom =1.25*( F2 / C1 )+H
9. Tmax =π*( D1 - B )*tg (10 ° )
11. S3 = T - H
12. F3 = C1 * S3
14. N calc =( L2 - H )/( H +F3 / C1 - F2 / C1 )
16.C = C1 / N
17. L0 = N * T + H
18. L3 = N * H + H
19. F2 = C * L0 - C * L2
21. F1 = C * L0 - C * L1
22. N1 = N +1.5
23. A =arctg ( T /( π *( D1 - H )))
24. L develop =π* N1 *( D1 - H )/cos ( A )
25. Q =H*B * Ldiv *7.85/106
Thermo-mechanical treatment
Without exception, all spring steels are subjected to thermomechanical treatment. After it, strength and wear resistance can increase 2 times. The product is shaped in an annealed state, when the steel has the maximum possible softness, after which it is heated to 830-870 C and cooled in an oil or water environment (only for grade 60 CA). The resulting martensite is tempered at a temperature of 480 ºC.
All requirements and recommendations for this type are described in GOST 14959-79. Based on them, the company develops more detailed technological sheets that meet narrow parameters.
Source of the article: https://prompriem.ru/stati/pruzhinnaya-stal.html
Shear modulus of copper - Metalworker's Handbook
All solids, both crystalline and amorphous, have the property of changing their shape under the influence of force applied to them. In other words, they are subject to deformation. If a body returns to its original size and shape after the external force ceases its influence, then it is called elastic, and its deformation is considered elastic.
For any body, there is a limit to the applied force, after which the deformation ceases to be elastic, the body does not return to its original shape and original dimensions, but remains in a deformed state or collapses. The theory of elastic deformations of bodies was created at the end of the 17th century by the British scientist R. Hooke and developed in the works of his compatriot Thomas Young.
Hooke's and Young's law and coefficient, which determine the degree of elasticity of bodies, were named in their honor, respectively. It is actively used in engineering during calculations of the strength of structures and products.
Young's modulus
Characteristics of spring steels
Spring steels are characterized by increased yield strength (δB) and elasticity. This is the most important characteristic of metal - to withstand mechanical loads without changing its original shape. Those. a metal subjected to tension or, conversely, compression (elastic deformation), after removing the acting forces from it, must remain in its original shape (without residual deformation).
Types and scope of spring steel
Based on the presence of additional properties, spring steel is divided into alloy (stainless) and carbon. Alloy steel is based on carbon steel with a C content of 65-85% and is alloyed with 4 main elements, all or selectively, each of which brings its own characteristics:
Chromium - at a concentration of more than 13%, works to ensure the corrosion resistance of the metal. With a chromium concentration of about 30%, the product can work in aggressive environments: acidic (except sulfuric acid), alkaline, aqueous. Corrosion spring steel is always alloyed with a second accompanying element - tungsten and/or manganese. Operating temperature up to 250 °C.
Tungsten is a refractory substance. When its powder gets into the melt, it forms numerous crystallization centers, crushing the grain, which leads to increased plasticity without loss of strength. This brings its advantages: the quality of such a structure remains very high during heating and intense abrasion of the surface. During heat treatment, this element retains its fine-grained structure and eliminates softening of steel during heating (during operation) and dislocation. During hardening, it increases hardenability, as a result of which the structure becomes homogeneous to a greater depth, which in turn increases the service life of the product.
Manganese and silicon usually participate in mutual doping, and the ratio always increases in favor of manganese, up to about 1.5 times. That is, if the silicon content is 1%, then manganese is added in an amount of 1.1-1.5%.
Refractory silicon is a non-carbide-forming element. When it enters the melt, it is one of the first to take part in crystallization, pushing carbon carbides to the grain boundaries, which accordingly leads to strengthening of the metal.
Manganese can be called a structure stabilizer. By simultaneously distorting the metal lattice and strengthening it, manganese eliminates the excessive strength of silicon.
In some steel grades (when the product is operating in high-temperature conditions, at temperatures above 300 ºC), nickel is added to the steel. It eliminates the formation of chromium carbides along grain boundaries, which lead to matrix destruction.
Vanadium can also be an alloying element, its function is similar to that of tungsten.
Spring brands specify the element copper; its content should not exceed 0.15%. Since copper, being a low-melting substance, concentrates at the grain boundaries, reducing strength.
Spring brands include: 50HG, 3K-7, 65G, 65GA, 50HGFA, 50HFA, 51HFA, 50HSA, 55S2, 55S2A, 55S2GF, 55HGR, 60G, 60S2, 60S2A, 605, 70, 70G, 75, 80, 85, 60С2ХА , 60S2HFA, 65S2VA, 68A, 68GA, 70G2, 70S2XA, 70S3A, 70HGFA, SH, SL, SM, DM, DN, KT-2.
Grades of such steel are used for the manufacture of not only springs and leaf springs, although this is their main purpose, which characterizes the main property. They are used wherever there is a need to provide the product with elasticity, ductility and strength at the same time. All parts made from these grades are subject to tension and compression. Many of them experience loads that periodically replace each other, and with a huge cyclic frequency. This:
- bearing housings that experience compression and tension at each point with high frequency;
- friction discs experiencing dynamic loads and compression;
- thrust washers, most of the time they experience compression loads, but a sharp change in tension can also be added to them;
- brake bands, for which one of the main tasks is elasticity under repeated stretching. With this dynamic of increased aging and wear, stronger steel (with less elasticity) is susceptible to rapid aging and sudden failure.
Elastic modulus of different steel grades
Spring steel alloys have the greatest ability to resist deformation. These materials are characterized by high yield strength. The value shows the stress at which the deformation increases without external influences, for example, when bending and twisting.
The elasticity characteristics of steel depend on alloying elements and the structure of the crystal lattice. Carbon imparts hardness to the steel alloy, but in high concentrations it reduces ductility and springiness. The main alloying additives that increase elastic properties: silicon, manganese, nickel, tungsten.
Often, the desired indicators can be achieved only with the help of special heat treatment modes. In this way, all fragments of the part will have uniform fluidity indicators, and weak areas will be eliminated. Otherwise, the product may break, burst or crack. Grades 60G and 65G have such characteristics as tensile strength, viscosity, wear resistance, they are used for the manufacture of industrial springs and musical strings.
The metallurgical industry has created several hundred grades of steel with different elastic moduli. The table shows the characteristics of popular alloys.
Table of strength moduli of steel grades
| Name of steel | Young's modulus of elasticity, 10¹² Pa | Shear modulus G, 10¹² Pa | Modulus of bulk elasticity, 10¹² Pa | Poisson's ratio, 10¹²·Pa |
| Low carbon steel | 165…180 | 87…91 | 45…49 | 154…168 |
| Steel 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Steel 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Steel 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Steel 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65G | 235…275 | 112…124 | 81…85 | 208…214 |
| X12MF | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| R6M5 | 305…320 | 147…151 | 98…102 | 294…300 |
| P9 | 320…330 | 155…162 | 104…110 | 301…312 |
| P18 | 325…340 | 140…149 | 105…108 | 308…318 |
| R12MF5 | 297…310 | 147…152 | 98…102 | 276…280 |
| U7, U8 | 302…315 | 154…160 | 100…106 | 286…294 |
| U9, U10 | 320…330 | 160…165 | 104…112 | 305…311 |
| U11 | 325…340 | 162…170 | 98…104 | 306…314 |
| U12, U13 | 310…315 | 155…160 | 99…106 | 298…304 |
Modulus of elasticity for metals and alloys
| Name of material | Elastic modulus value, 10¹² Pa |
| Aluminum | 65—72 |
| Duralumin | 69—76 |
| Iron, carbon content less than 0.08% | 165—186 |
| Brass | 88—99 |
| Copper (Cu, 99%) | 107—110 |
| Nickel | 200—210 |
| Tin | 32—38 |
| Lead | 14—19 |
| Silver | 78—84 |
| Gray cast iron | 110—130 |
| Steel | 190—210 |
| Glass | 65—72 |
| Titanium | 112—120 |
| Chromium | 300—310 |
Elasticity of steels
| Name of steel | Elastic modulus value, 10¹² Pa |
| Low carbon steel | 165—180 |
| Steel 3 | 179—189 |
| Steel 30 | 194—205 |
| Steel 45 | 211—223 |
| Steel 40Х | 240—260 |
| 65G | 235—275 |
| X12MF | 310—320 |
| 9ХС, ХВГ | 275—302 |
| 4Х5МФС | 305—315 |
| 3Х3М3Ф | 285—310 |
| R6M5 | 305—320 |
| P9 | 320—330 |
| P18 | 325—340 |
| R12MF5 | 297—310 |
| U7, U8 | 302—315 |
| U9, U10 | 320—330 |
| U11 | 325—340 |
| U12, U13 | 310—315 |
Work order
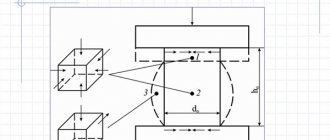
Determination of the shear modulus by the spring stretching method
- Raise the bracket with the spring so that the bracket with the photosensor does not interfere with the measurements. Hang a mass of mass m1 on the spring. Using a ruler, note the location of the lower plane of the load x1.
- Hang a mass of mass m2 on the spring. Using a ruler, note the location of the bottom plane of the weight x2.
- Determine the elongation of the spring x = x1-x2.
- Using a caliper, measure the diameter of the spring D and the diameter of the rod from which the spring is made d.
- Determine the shear modulus using formula (9), in which F = mg is the force that stretches the spring, m = m2- m1, N is the number of turns in the spring.
Determination of shear modulus using a spring pendulum
- Hang one of the springs under study on the bracket. Hang a weight on the spring.
- Fix the bracket with a vertically suspended spring on a vertical stand in such a way that the stacked weight suspended from the spring, with its lower plane, coincides with the optical axis of the photosensor fixed in the lower part of the stand (the optical axis of the photosensor coincides with the marks on the photosensor).
- Press the “NETWORK” button of the unit. In this case, the display panel should turn on.
- Lift the weight up a little and release. In this case, the load begins to oscillate on the spring. Press the “START” button, determine the time value of 20 oscillations of the load using the timer.
- Press the "STOP" button.
- Determine the period of oscillation of the load using the formula:
T=\frac{t}{n}
t – oscillation time;
n – number of oscillations.
- Determine the shear modulus using formula (10)
Determine the relative error of shear modulus measurements carried out by various methods. Compare the values of the shear modulus obtained experimentally by different methods with the values given in the table on the installation. Draw a conclusion about the grade of steel from which the spring is made.