Most often, metals have crystal lattices of the following types: Body-centered cubic or abbreviated bcc (lead, tungsten) 9 atoms; Face-centered cubic (fcc) (silver, gold) 14 atoms; hexagonal close-packed (hcp) (magnesium, zinc). FCC and HCP lattices are more compact than bcc.
All metals are crystalline bodies that have a certain type of crystal lattice, consisting of low-mobility positively charged ions, between which free electrons move (the so-called electron gas
).
This type of structure is called a metallic bond
.
The type of lattice is determined by the shape of an elementary geometric body, the repeated repetition of which along three spatial axes forms the lattice of a given crystalline body.
Metals have relatively complex types of cubic lattices - body-centered (bcc) and face-centered (fcc) cubic lattices.
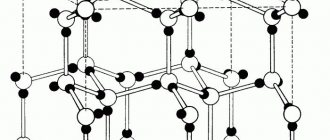
The basis of the bcc lattice is an elementary cubic cell (Fig. 1.2, b), in which positively charged metal ions are located at the vertices of the cube, and another atom in the center of its volume, i.e. at the intersection of its diagonals. Iron, chromium, vanadium, tungsten, molybdenum and other metals have this type of lattice in certain temperature ranges.
In an fcc lattice (Fig. 1.2, c), the unit cell is a cube with centered faces. Iron, aluminum, copper, nickel, lead and other metals have a similar lattice.
The third common type of close-packed lattices is hexagonal close-packed (HCP, Fig. 1.2, d). The GPU cell consists of spaces spaced from each other by a parameter c
parallel centered hexagonal bases. Three ions (atoms) are located on the middle plane between the bases.
For hexagonal lattices, the ratio of the parameter with
/
a
is always greater than one. Magnesium, zinc, cadmium, beryllium, titanium, etc. have such a lattice.
Didn't find what you were looking for? Use the search:
Best sayings:
Only sleep brings a student closer to the end of the lecture.
And someone else's snoring alienates him. 8588 – | 7405 – or read all.
91.146.8.87 © studopedia.ru Not the author of the materials posted. But it provides free use. Is there a copyright violation? Write to us | Feedback.
Disable adBlock! and refresh the page (F5)
very necessary
One of the most common materials that people have always preferred to work with has been metal. In each era, preference was given to different types of these amazing substances. Thus, the IV-III millennium BC is considered the Chalcolithic, or Copper Age. Later it is replaced by bronze, and then the one that is still relevant today comes into force - iron.
Today it is generally difficult to imagine that it was once possible to do without metal products, because almost everything, from household items, medical instruments to heavy and light equipment, consists of this material or includes individual parts from it. Why did metals manage to gain such popularity? Let’s try to figure out what the features are and how this is inherent in their structure.
General concept of metals
"Chemistry. 9th grade" is a textbook used by schoolchildren. It is here that metals are studied in detail. A large chapter is devoted to the consideration of their physical and chemical properties, because their diversity is extremely great.
Read also: Caprolon or polyurethane, which is better?
It is from this age that it is recommended to give children an idea of these atoms and their properties, because teenagers can already fully appreciate the significance of such knowledge. They see perfectly well that the variety of objects, machines and other things around them is based on a metallic nature.
What is metal? From the point of view of chemistry, these atoms are usually classified as those that have:
- a small number of electrons at the outer level;
- exhibit strong restorative properties;
- have a large atomic radius;
- As simple substances, they have a number of specific physical properties.
The basis of knowledge about these substances can be obtained by considering the atomic-crystalline structure of metals. It is this that explains all the features and properties of these compounds.
In the periodic table, most of the entire table is allocated to metals, because they form all the secondary subgroups and the main ones from the first to the third group. Therefore, their numerical superiority is obvious. The most common are:
All metals have a number of properties that allow them to be combined into one large group of substances. In turn, these properties are explained precisely by the crystalline structure of metals.
Physical properties of copper:
| 204 | Atomic radius (calculated) | 145 pm |
| 205 | Empirical atomic radius* | 135 pm |
| 206 | Covalent radius* | 132 pm |
| 207 | Ion radius (crystalline) | Cu + (in parentheses the coordination number is indicated - a characteristic that determines the number of nearest particles (ions or atoms) in a molecule or crystal) |
| 208 | Van der Waals radius | 140 pm |
| 209 | Electrons, Protons, Neutrons | 29 electrons, 29 protons, 35 neutrons |
| 210 | Family (block) | d-family element |
| 211 | Period in the periodic table | 4 |
| 212 | Group on the periodic table | 11th group (according to the old classification - a secondary subgroup of the 1st group) |
| 213 | Emission spectrum | |
| 306 | Electron affinity energy of an atom | 119.235(4) kJ/mol (1.23578(4) eV) |
| 400 | Physical properties | |
| 401 | Density* | 8.96 g/cm 3 (at 20 °C and other standard conditions, state of matter - solid), |
8.02 g/cm 3 (at a melting point of 1084.62 °C and other standard conditions, the state of the substance is liquid),
7.962 g/cm 3 (at 1127 °C and other standard conditions, the state of matter is liquid), 7.881 g/cm 3 (at 1227 °C and other standard conditions, the state of matter is liquid), 7.799 g/cm 3 (at 1327 °C and other standard conditions, state of matter - liquid), 7.471 g/cm 3 (at 1727 °C and other standard conditions, state of matter - liquid), 7.307 g/cm 3 (at 1927 °C and other standard conditions, state substances - liquid),
7.225 g/cm 3 (at 2027 °C and other standard conditions, the state of matter is liquid), 7.102 g/cm 3 (at 2177 °C and other standard conditions, the state of matter is liquid)
Properties of metals
The specific properties of the substances in question include the following.
- Metallic shine. All representatives of simple substances have it, and most have the same silvery-white color. Only a few (gold, copper, alloys) are different.
- Malleability and plasticity - the ability to deform and recover quite easily. It is expressed to different degrees in different representatives.
- Electrical and thermal conductivity are one of the main properties that determine the areas of application of a metal and its alloys.
The crystalline structure of metals and alloys explains the reason for each of the indicated properties and speaks about their severity in each specific representative. If you know the features of such a structure, then you can influence the properties of the sample and adjust it to the desired parameters, which is what people have been doing for many decades.
1.5. Allotropy of metals
Some metals, for example, iron, titanium, tin, etc., are capable of changing their crystal structure upon reaching certain temperatures, i.e., changing the type of unit cell of their crystal lattice. This phenomenon is called allotropy
or
polymorphism
, and the transitions themselves from one crystalline structure to another are called allotropic or polymorphic.
In Fig. Figure 1.7 shows the change free energy
F
as a function of temperature
t
for two variants of the crystalline structure of iron: bcc (curve
1
) and fcc (curve
2).
In the temperature range 911-1392 o C, iron has an fcc lattice, since in this case its free energy is less. At t 1392°C, it should have a bcc lattice, which has less free energy.
Atomic crystal structure of metals
What is this structure, what is it characterized by? The name itself suggests that all metals are crystals in the solid state, that is, under normal conditions (except for mercury, which is a liquid). What is a crystal?
This is a conventional graphic image constructed by intersecting imaginary lines through the atoms that line up the body. In other words, every metal is made up of atoms. They are located in it not chaotically, but very correctly and consistently. So, if you mentally combine all these particles into one structure, you will get a beautiful image in the form of a regular geometric body of some shape.
This is what is commonly called the crystal lattice of a metal. It is very complex and spatially voluminous, therefore, for simplicity, not all of it is shown, but only a part, an elementary cell. A set of such cells, collected together and reflected in three-dimensional space, forms crystal lattices. Chemistry, physics and metallurgy are sciences that study the structural features of such structures.
The unit cell itself is a set of atoms that are located at a certain distance from each other and coordinate a strictly fixed number of other particles around themselves. It is characterized by packing density, distance between constituent structures, and coordination number. In general, all these parameters are characteristics of the entire crystal, and therefore reflect the properties exhibited by the metal.
Read also: How to open a furniture stapler
There are several types of crystal lattices. They all have one feature in common: the nodes contain atoms, and inside there is a cloud of electron gas, which is formed by the free movement of electrons inside the crystal.
General structure
Metals are solid substances with a crystalline structure. The exception is mercury, a liquid metal. Crystal lattices are metal atoms ordered in a certain way. Each atom consists of a positively charged nucleus and several negatively charged electrons. Metal atoms don't have enough electrons, so they are ions.
A unit of a crystal lattice is an elementary crystal cell, in the conventional nodes and on the faces of which there are positively charged ions. They are held together by metallic bonds that arise due to the random movement of electrons separated from the atoms (due to which the atoms turned into ions).
Rice. 1. Metal connection diagram.
The free movement of electrons determines the electrical and thermal conductivity of metals.
Types of crystal lattices
Fourteen lattice structure options are usually combined into three main types. They are as follows:
- Body-centered cubic.
- Hexagonal close-packed.
- Face-centered cubic.
The crystal structure of metals was studied only through electron microscopy, when it became possible to obtain high magnification images. And the classification of types of lattices was first given by the French scientist Bravais, by whose name they are sometimes called.
Body-centered lattice
The structure of the crystal lattice of metals of this type is the following structure. This is a cube with eight atoms at its nodes. Another one is located in the center of the free internal space of the cell, which explains the name “body-centered”.
This is one of the options for the simplest structure of the unit cell, and therefore the entire lattice as a whole. The following metals have this type:
- molybdenum;
- vanadium;
- chromium;
- manganese;
- alpha iron;
- beta iron and others.
The main properties of such representatives are a high degree of malleability and ductility, hardness and strength.
Types of gratings
Unit crystal cells can have different configurations. In this regard, three types of crystal lattices are distinguished:
- body-centered (bcc) cubic – consists of 9 ions;
- face-centered (fcc) cubic – includes 14 ions;
- hexagonal close-packed (hcp) - consists of 17 ions.
A bcc is a cube with an atom at its nodes. The ninth ion is located in the center of the cube, at the intersection of the diagonals. This type is typical for iron, molybdenum, chromium, tungsten, and vanadium.
The elementary crystalline cell of the fcc type is a cube with ions at the nodes and in the middle of each face - at the intersection of the diagonals. Copper, silver, aluminum, lead, and nickel have this structure.
The third type has the form of a hexagonal prism, the nodes of which contain six ions on each side. One ion is located in the middle between the six nodes. In the middle of the prism between the hexagonal faces there is an equilateral triangle, which is made up of three ions.
Rice. 2. Types of gratings.
A metal can contain a large number of atomic structure defects. Defects affect the properties of the metal.
Face-centered lattice
The crystal structure of metals having a face-centered cubic lattice is the following structure. This is a cube that includes fourteen atoms. Eight of them form lattice nodes, and another six are located, one on each face.
They have a similar structure:
The main distinctive properties are shine of different colors, lightness, strength, malleability, increased resistance to corrosion.
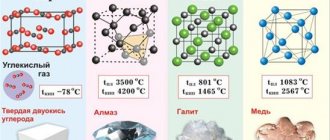
Copper crystal lattice:
500
| Crystal cell | ||
| 511 | Crystal grid #1 | |
| 512 | Lattice structure | Cubic face centered |
| 900 | additional information | |
| 901 | CAS number | 7440-50-8 |
Defects in the crystal structure of metals
However, all types of cells considered may also have natural shortcomings, or so-called defects. This may be due to various reasons: foreign atoms and impurities in metals, external influences, and so on.
Therefore, there is a classification that reflects the defects that crystal lattices may have. Chemistry as a science studies each of them in order to identify the cause and method of elimination so that the properties of the material are not changed. So, the defects are as follows.
- Spot. They come in three main types: vacancies, impurities or dislocated atoms. They lead to deterioration of the magnetic properties of the metal, its electrical and thermal conductivity.
- Linear or dislocation. There are edge and screw ones. They deteriorate the strength and quality of the material.
- Surface defects. Affects the appearance and structure of metals.
Currently, methods have been developed to eliminate defects and obtain pure crystals. However, it is not possible to completely eradicate them; an ideal crystal lattice does not exist.
1.4. Anisotropy in crystals
Under Anisotropy
understands the dissimilarity of mechanical and other properties in crystalline bodies along different crystallographic directions. It is a natural consequence of the crystal structure, since the atomic density is different on different crystallographic planes and along different directions.
For example, in cubic lattices (see Fig. 1.2, b, c) there are fewer atoms in the directions along the edges than along the diagonals of the cube in the bcc lattice or the diagonals of the faces in the fcc lattice. There are fewer atoms on the planes passing through the faces of the bcc and fcc lattices than on the diagonal planes.
Since the mechanical, physical and chemical properties along different directions depend on the density of the atoms located on them, the listed properties along different directions in crystalline solids should not be the same.
Anisotropy appears only within one single crystal or crystallite grain. In polycrystalline solids it is not observed due to the averaging of properties in each direction for a huge number of grains randomly oriented relative to each other. Therefore, real metals are quasi-isotropic bodies, that is, pseudo-isotropic.
Rice. 1.5. Unit cell of a bcc lattice
Shear in a crystal occurs most easily along atomic planes with the densest packing of atoms. Consider a body-centric cubic lattice (BCC) (Fig. 1.5):
Rice. 1.6. BCC lattice planes
The importance of knowledge about the crystalline structure of metals
From the above material, it is obvious that knowledge about the fine structure and structure makes it possible to predict the properties of the material and influence them. And the science of chemistry allows you to do this. The 9th grade of a general education school places emphasis in the learning process on developing in students a clear understanding of the importance of the fundamental logical chain: composition - structure - properties - application.
Read also: How to attach a vacuum cleaner to an angle grinder
Information about the crystalline structure of metals very clearly illustrates this dependence and allows the teacher to clearly explain and show children how important it is to know the fine structure in order to correctly and competently use all the properties.
Content:
1.3. Crystallographic directions and planes
The orderliness of the crystal structure in the spatial lattice makes it possible to distinguish individual crystallographic directions and planes.
Crystallographic planes are, for example, the planes of the faces of cubes (Fig. 1.4, b), as well as their various diagonal planes together with the atoms located on them (Fig. 1.4, c, d). For hcp lattices, the crystallographic planes can be the planes of the bases (Fig. 1.2, d).
To determine the index of any direction, it is necessary to find the index of the atom closest to a given reference point located in a given direction. For example, the index of the nearest atom along the OX
indicated by the numbers 100 (Fig. 1.4,a).
This and the numbers represent the coordinates of the mentioned atom relative to point O, expressed through the number of parameters along the OX, OY
and
OZ
, respectively.
The indices of the direction OX and directions parallel to it are designated [100]. Accordingly directions OY
and
OZ
are designated [010] and [001].
of the XOZ, XOY,
and
YOZ
faces are designated [101], [110], and [011]. Using this technique, you can determine the index of any direction. For example, the direction index along the diagonal of a cube is expressed as follows: [111].
Indices of planes parallel to XOZ
and
YOZ,
the expressions (010) and (100) will appear (Fig. 1.4, b). The index of the vertical diagonal plane of the cube will be expressed through (110), (Fig. 1.2, c), and the index of the inclined plane, intersecting with all three coordinate axes at a distance of one parameter, will take the form (111) (see Fig. 1.4, d).
Definition of crystal lattice
As we know, all material substances can exist in three basic states: liquid, solid, and gaseous. True, there is also a state of plasma, which scientists consider no less than the fourth state of matter, but our article is not about plasma. The solid state of a substance is therefore solid because it has a special crystalline structure, the particles of which are in a certain and clearly defined order, thus creating a crystal lattice. The structure of the crystal lattice consists of repeating identical elementary cells: atoms, molecules, ions, and other elementary particles connected by various nodes.
Note:
205* The empirical radius of the copper atom according to [1] and [3] is 128 pm.
206* Covalent radius of copper according to [1] and [3] is 132±4 pm and 117 pm, respectively.
401* The density of copper according to [3] is 8.92 g/cm 3 (at 0 °C and under normal conditions, the state of the substance is a solid).
402* The melting point of copper according to [3] and [4] is 1083.4 °C (1356.55 K, 1982.12 °F) and 1083 °C (1356.15 K, 1981.4 °F), respectively.
403* The boiling point of copper according to [3] and [4] is 2567 °C (2840.15 K, 4652.6 °F) and 2543 °C (2816.15 K, 4609.4 °F), respectively.
407* The specific heat of fusion (enthalpy of fusion ΔHmelt) of copper according to [3] and [4] is 13.01 kJ/mol and 13 kJ/mol, respectively.
408* The specific heat of evaporation (enthalpy of boiling ΔHboiling) of copper according to [3] and [4] is 304.6 kJ/mol and 302 kJ/mol, respectively.
Source
Types of crystal lattices
Depending on the particles of the crystal lattice, there are fourteen types of it, here are the most popular of them:
- Ionic crystal lattice.
- Atomic crystal lattice.
- Molecular crystal lattice.
- Metal crystal lattice.
Next, we will describe in more detail all types of crystal lattice.
Atomic crystal lattice
Substances with an atomic crystal lattice, as a rule, have strong covalent bonds in their nodes consisting of atoms themselves. A covalent bond occurs when two identical atoms share fraternal electrons with each other, thus forming a common pair of electrons for neighboring atoms. Because of this, covalent bonds bind atoms tightly and evenly in a strict order - perhaps this is the most characteristic feature of the structure of the atomic crystal lattice. Chemical elements with similar bonds can boast of their hardness and high melting point. Chemical elements such as diamond, silicon, germanium, and boron have an atomic crystal lattice.
Additional information:
| 402 | Melting temperature* | 1084.62 °C (1357.77 K, 1984.32 °F) |
| 403 | Boiling temperature* | 2562 °C (2835 K, 4643 °F) |
| 404 | Sublimation temperature | |
| 405 | Decomposition temperature | |
| 406 | Self-ignition temperature of a gas-air mixture | |
| 407 | Specific heat of fusion (enthalpy of fusion ΔHpl)* | 13.26 kJ/mol |
| 408 | Specific heat of evaporation (enthalpy of boiling ΔHboiling)* | 300.4 kJ/mol |
| 409 | Specific heat capacity at constant pressure | 0.384 J/g K (at 20 °C) |
| 410 | Molar heat capacity | 24.44 J/(K mol) |
| 411 | Molar volume | 7.1 cm³/mol |
| 412 | Thermal conductivity | 401 W/(mK) (at standard conditions), 401 W/(mK) (at 300 K) |
| 413 | Thermal expansion coefficient | 16.5 µm/(MK) (at 25 °C) |
| 414 | Thermal diffusivity coefficient | |
| 415 | Critical temperature | |
| 416 | Critical pressure | |
| 417 | Critical Density | |
| 418 | Triple point | |
| 419 | Vapor pressure (mmHg) | 0.000000001 mmHg (at 672°C), 0.00000001 mmHg. (at 727°C), 0.0000001 mmHg. (at 787°C), 0.000001 mmHg. (at 857°C), 0.00001 mmHg. (at 934°C), 0.0001 mmHg. (at 1025°C), 0.001 mmHg. (at 1133°C), 0.01 mmHg. (at 1264°C), 0.1 mmHg. (at 1419°C), 1 mmHg. (at 1617°C), 10 mmHg. (at 1910°C), 100 mmHg. (at 2312°C) |
| 420 | Vapor pressure (Pa) | 1 Pa (at 1509 K), 100 kPa (at 2834 K) |
| 421 | Standard enthalpy of formation ΔH | 0 kJ/mol (at 298 K, for the state of matter - solid), 338 kJ/mol (at 298 K, for the state of matter - gas) |
| 422 | Standard Gibbs energy of formation ΔG | 0 kJ/mol (at 298 K, for the state of matter - solid) |
| 423 | Standard entropy of matter S | 33.15 J/(mol K) (at 298 K, for the state of matter - solid), 166.3 J/(mol K) (at 298 K, for the state of matter - gas) |
| 424 | Standard molar heat capacity Cp | 24.4 J/(mol K) (at 298 K, for the state of matter - solid), |
Metal crystal lattice
The type of bond of a metal crystal lattice is more flexible and ductile than the ionic one, although in appearance they are very similar. Its distinctive feature is the presence of positively charged cations (metal ions) at lattice sites. Between the nodes live electrons that participate in the creation of the electric field; these electrons are also called electric gas. The presence of such a structure of a metal crystal lattice explains its properties: mechanical strength, heat and electrical conductivity, fusibility.
1.1. Amorphous and crystalline bodies
In solids, atoms can be arranged in space in two ways:
Amorphous substances have the formal characteristics of solids, i.e. they are able to maintain constant volume and shape. However, they do not have a specific melting or crystallization point.
The outer electron orbits of the atoms touch, so the packing density
atoms in the crystal lattice is very large.
In crystallites, short- and long-range orders are observed. This means the presence of an ordered arrangement and stability as its nearest neighbors surrounding a given atom ( short-range order
), and atoms located at significant distances from it, up to the grain boundaries (
long-range order
).
Rice. 1.1. Arrangement of atoms in crystalline (a) and amorphous (b) matter
Due to diffusion
individual atoms can leave their places in the nodes of the crystal lattice, but the order of the crystal structure as a whole is not disrupted.